Let’s talk a bit about functors. Functors are fun!

What’s a functor? I already gave the short definition: a structure-preserving mapping between categories. Let’s be a bit more formal. What does the structure-preserving property mean?

A functor F from category C to category D is a mapping from C to D that:

• Maps each member to an object .
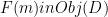• Maps each arrow to an arrow , where:
  • . (Identity is preserved by the functor mapping of morphisms.)
  • . (Associativity is preserved by the Functor mapping of morphisms.)

That’s the standard textbook gunk for defining a functor. But if you look back at the original definition of a category, you should notice that this looks familiar. In fact, it’s almost identical to the definition of the necessary properties of arrows!

We can make functors much easier to understand by talking about them in the language of categories themselves. Functors are arrows between a category of categories.

There’s a kind of category, called a small category. (I happen to dislike the term “small” category; I’d prefer something like “well-behaved”.) A small category is a category C where Obj(C) and Mor(C) are sets, not proper classes. Alas, more definitions; in set theory, a class is a collection of sets that can be defined by a non-paradoxical property that all of its members share. Some classes are sets of sets; some classes are not sets; they lack some of the required properties of sets – but still, the class is a collection with a well-defined, non-paradoxical, unambiguous property. If a class isn’t a set of sets, but just a collection that isn’t a set, then it’s called a proper class.

Any category whose collections of objects and arrows are sets, not proper classes, are called small categories. Small categories are, basically, categories that are well-behaved – meaning that their collections of objects and arrows don’t have any of the obnoxious properties that would prevent them from being sets.

The small categories are, quite beautifully, the objects of a category called Cat. (For some reason, category theorists like three-letter labels.) The arrows of Cat are the functors: Functors are morphisms between small categories. Once you wrap you head around that, then the meaning of a functor, and the meaning of a structure-preserving transformation become extremely easy to understand.

Functors come up over and over again, all over mathematics. They’re an amazingly useful notion. I was looking for a list of examples of things that you can describe using functors, and found a really wonderful list on wikipedia.. I highly recommend following that link and taking a look at the list. I’ll just mention one particularly interesting example: groups and group actions.

If you’ve been reading GM/BM long enough, you’ll remember my posts on group theory, and how long it took for me to work up to the point where I could really define what symmetry meant, and how every symmetric transformation was actually a group action. Category theory makes that much easier.

Every group can be represented as a category with a single object. A functor from the category of a group to the category of Sets is a group action on the set that is the target of the functor. Poof! Symmetry. (This paragraph was modified to correct some ambiguous wording; the ambiguity was pointed out by commenter “Cat lover”.)

Since symmetry means structure-preserving transformation; and a functor is a structure preserving transformation – well, they’re almost the same thing. The functor is an even more general abstraction of that concept: group symmetry is just one particular case of a functor transformation. Once you get functors, understanding symmetry is easy. And so are lots of other things.

And of course, you can always carry these things further. There is a category of functors themselves; and notions which can be most easily understood in terms of functors operating on the category of functors!

By now, it should be sort of clear why category theory is affectionately known as abstract nonsense. Category theory operates at a level of abstraction where almost anything can be wrapped up in it; and once you’ve wrapped something up in a category, almost anything you can do with it can itself be wrapped up asa category – levels upon levels, categories of categories, categories of functors on categories of functors on categories, ad infinitum. And yet, it makes sense. It captures a useful, comprehensible notion. All that abstraction, to the point where it seems like nothing could possibly come out of it. And then out pops a piece of beautiful crystal.

For me, the frustrating thing about learning category theory was that
it seemed to be full of definitions, but that I couldn’t see why I should care.
What were these category things, and what could I really talk about using this
strange new mathematical language of categories?

To avoid that in my presentation, I’m going to show you a couple of examples up front of things we can talk about using the language of category theory: sets, partially ordered sets, and groups.

Sets as a Category

We can talk about sets using category theory. The objects in the category of sets are, obviously, sets. Arrows in the category of sets are total functions between sets.

Let’s see how these satisfy our definition of categories:

• Given a function f from set A to set B, it’s represented by an arrow f : A → B.
• º is function composition. It meets the properties of a categorical º:
  • Associativity: function composition over total functions is associative; we know that from set theory.
  • Identity: for any set S, 1_S is the identity function: (∀ i ∈ S) 1_S(i) = i. It should be pretty obvious that for any f : S → T, f º 1_S = f; and 1_T º f = f.

Partially Ordered Sets

Partially ordered sets (that is, sets that have a “<=" operator) can be described as a category, usually called PoSet. The objects are the partially ordered sets; the arrows are monotonic functions (a function f is monotonic if (∀ x,y &isin domain(x)) x <= y ⇒ f(x) <= f(y).). Like regular sets, º is function composition.

It’s pretty easy to show the associativity and identity properties; it’s basically the same as for sets, except that we need to show that º preserves the monotonicity property. And that’s not very hard:

• Suppose we have arrows f : A → B, g : B → C. We know that f and g are monotonic
  functions.

• Now, for any pair of x and y in the domain of f, we know that if x <= y, then f(x) <= f(y).
• Likewise, for any pair s,t in the domain of g, we know that if s <= t, then g(s) <= g(t).
• Put those together: if x <= y, then f(x) <= f(y). f(x) and f(y) are in the domain of g, so if (f(x) <= f(y)) then we know g(f(x)) <= g(f(y)).

Groups as a Category

There is a category Grp where the objects are groups; group homomorphisms are arrows. Homomorphisms are structure-preserving functions between sets; so function composition of those structure-preserving functions is the composition operator º. The proof that function composition preserves structure is pretty much the same as the proof we just ran through for partially ordered sets.

Once you have groups as a category, then you can do something very cool. If groups are a category, then functors over groups are symmetric transformations. Walk it through, and you’ll see that it fits. What took me a week of writing to be able to explain when I was talking about group theory can be stated in one sentence using the language of category theory. That’s a perfect example of why cat theory is useful: it lets you say some very important, very complicated things in very simple ways.

Miscellaneous Comments

There’ve been a couple of questions about from category theory skeptics in the comments. Please don’t think I’m ignoring you. This stuff is confusing enough for most people (me included) that I want to take it slowly, just a little bit at a time, to give readers an opportunity to digest each bit before going on to the next. I promise that I’ll answer your questions eventually!

One of the things that I find niftiest about category theory is category diagrams. A lot of things that normally turn into complex equations or long-winded logical statements can be expressed in diagrams by capturing the things that you’re talking about in a category, and then using category diagrams to express the idea that you want to get accross.

A category diagram is a directed graph, where the nodes are objects from a category, and the edges are morphisms. Category theorists say that a graph commutes if, for any two paths through arrows in the diagram from node A to node B, the composition of all edges from the first path is equal to the composition of all edges from the second path.

As usual, an example will make that clearer.

This diagram is a way of expression the associativy property of morphisms: f º (g º h) = (f º g) º h. The way that the diagram illustrates this is: (g º h) is the morphism from A to C. When we compose that with f, we wind up at D. Alternatively, (f º g) is the arrow from B to D; if we compose that with H, we wind up at D. The two paths: f º (A → C), and (B → D) &ordm h are both paths from A to D, therefore if the diagram commutes, they must be equal.

Let’s look at one more diagram, which we’ll use to define an interesting concept, the principal morphism between two objects. The principle morphism is a single arrow from A to B, and any composition of morphisms that goes from A to B will end up being equivalent to it.

In diagram form, a morphism m is principle if (∀ x : A → A) (∀ y : A → B), the following diagram commutes.

In words, this says that f is a principal morphism if for every endomorphic arrow x, and for every arrow y from A to B, f is is the result of composing x and y. There’s also something interesting about this diagram that you should notice: A appears twice in the diagram! It’s the same object; we just draw it in two places to make the commutation pattern easier to see. A single object can appear in a diagram as many times as you want to to make the pattern of commutation easy to see. When you’re looking at a diagram, you need to be a bit careful to read the labels to make sure you know what it means. (This paragraph was corrected after a commenter pointed out a really silly error; I originally said “any identity arrow”, not “any endomorphic arrow”.)

One more definition by diagram: x and y are a retraction pair, and A is a retract of B (written A < B) if the following diagram commutes:

That is, x : A → B, and y : B → A are a retraction pair if y º x = 1_A.

To get started, what is category theory?

Back in grad school, I spent some time working with a thoroughly insane guy named John Case who was the new department chair. When he came to the university, he brought a couple of people with him, to take temporary positions. One of them was a category theorist whose name I have unfortunately forgotten. That was the first I’d ever heard of cat theory. So I asked John what the heck this category theory stuff was. His response was “abstract nonsense”. I was astonished; a guy as wacky and out of touch with reality as John called something abstract nonsense? It turned out to be a classic quotation, attributed to one of the founders of category theory, Norman Steenrod. It’s not an entirely bad description.

Category theory is one of those fields of mathematics that fascinates me: where you take some fundamental concept, and abstract it down to its bare essentials in order to understand just what it really is, what it really means. Just like group theory takes the idea of an algebraic operation, strip it down to the bare minimum, and discovering the meaning of symmetry; category theory looks at what happens if you take the concept of a function as a mapping from one thing to another, and strip it down to the bare minimum, and see what you can discover?

The fundamental thing in category theory is an arrow, also called a morphism. A morphism is an abstraction of the concept of homomorphism, which I talked about a bit when I was writing about group theory. We take that concept of a function mapping from one set of values to another, and strip it down: the basic concept is something that provides a map from one thing to some other thing – and that’s all we want.

In classic style, we’ll define a category C as a tuple: (O, M, º), where:

• O, or Obj(C), is a set of objects. Objects are anything – we don’t care. Anything that we can define maps over.
• M, or Mor(C) is a set of arrows or morphisms. Every arrow has a unique source and a unique target, both of which are objects in M. Given two objects a and b in O, we also write Mor(a,b) for the set of morphisms from a to b. To talk about a specific morphism from a to b, we write it as “name : a → b”; as in “f : int → int”.
• º is a binary operation that is the abstraction of function composition; º is a mapping from (Mor(a,b), Mor(b,c)) to Mor(a,c). It’s got the basic properties of function composition:
  1. Associativity: (∀ f : a → b, g : b → c, h : c → d) h º (g º f) = (h º g) º f
  2. Identity: (∀ a,b ∈ O(C)) (exists 1_a, 1_b ∈ Mor(C)) (∀ f : a → b) 1_b º f = f = f º 1_a.

One neat little trick to simplify things is that we can actually throw away Obj(C), and replace it with the set of identity morphisms: since there is exactly one identity morphism per object, there’s no real need to distinguish between the identity morphism and the object. It’s a nice trick because it means that we have nothing but morphisms all the way down; but it’s really just a trick. We can talk about Obj(C); or Id(C); but we still need to be able to talk about the objects in some way, whether they’re just a subset of the morphisms, or something distinct.

Now, we get to something about category theory that I really don’t like. Category theory is front-loaded with rather a lot of definitions about different kinds of morphisms and different kinds of categories. The problem with that is that these definitions are very important, but we don’t have enough of the theory under our belts to be able to get much of a sense for why we should care about them, or what their intuitive meaning is. But that’s the way it goes sometimes; you have to start somewhere. It will make sense eventually, and you’ll see why these definitions matter.

There are a lot of special types of morphisms, defined by properties. Here’s the basic list:

• A monic (or monomorphism) is an arrow f : a → b such that (∀ g₁ , g₂: x → a) f º g₁ = f º g₂ ⇒ g₁ = g₂. (That is, if any two arrows composed with f in f º g end up at the same object only if they are the same.)
• An epic (or epimorphism) is an arrow f : a → b such that (∀ g₁ , g₂: b → x) g₁ º f = g₂ º f ⇒ g₁ = g₂. (This is almost the same as a monic, but it’s from the other side of the composition; instead of (f º g) in the definition, it’s (g º f).)
• An isomorphism is an arrow f : a → b such that (∃ g : b → a) f º g = 1_b ∧ g º f = 1_a.
• An endomorphism is an arrow f : a → b such that a = b.
• An automorphism is an arrow that is both an endmorphism and an isomorphism.

One last definition, just because it gives me a chance to point out something useful about category theory. A functor is a morphism in the category of all categories. What that means is that it’s a structure-preserving mapping between categories. It’s neat in a theoretical way, because it demonstrates that we’re already at a point where we’re seeing how category theory can make it easier to talk about something complicated: we’re using it to describe itself! But the concept of functor also has a lot of applications; in particular, the module system of my favorite programming language makes extensive use of functors.

In Ocaml, a module is something called a structure, which is a set of definitions with constrained types. One of the things you often want to be able to do is to write a piece of code in a way that allows you to make it parametric on some other structure. The way you do that is to write a functor: a “function” from a structure to a structure. For example, to implement a generic binary tree, you need a type of values that you’ll put in the tree; and an operation to compare values. The way you do that is to write a functor which takes a structure defining a type and a comparison operator, and mapping it to a structure which is an implementation of a binary tree for that type and comparison.

The Ocaml functor is a category theoretic functor: category theory provides an easy way to talk about the concept of the compile-time “function” from structure to structure.