I’ve written recently about several different crackpots who insist, for a variety of completely ridiculous reasons, that is wrong. But the other day, someone sent me a link to a completely serious site that makes a pretty compelling argument that
really is wrong.
The catch is that they aren’t saying that the value of is wrong. They’re saying that
is the wrong constant for talking about circles.
There’s a pretty good case for that. The fundamental measure that we use for a circle is the radius – and there are a lot of good reasons for that. But is based on the diameter: it’s the ratio of the circumference to the diameter. If you use the radius as the fundamental measure, and you go to define a circle constant, the natural choice isn’t
. It’s
. In the linked article, the author proposes naming this
.
It really does make a lot of sense. Look at basic mathematical systems that use , and you find an awful lot of 2s – and the argument is that those 2s are all over the place because of the fact that we’re using the wrong damned constant.
For example, what’s the equation for a fourier transform?
Why are those 2s there? Because is wrong. We should use
, which gives us the cleaner equations:
It’s no a big deal, but it does actually make those equations make more more sense. As we’ll see below, it actually helps to clarify the meaning of those equations!
So, suppose we decide to use as the fundamental circle constant. What effect does it really have? A whole lot of things actually make a lot of sense. What’s one full turn around a circle in radians?
. And that’s quite beautiful and natural. A quarter circle is
radians. That’s lovely.
What’s the width of a sin curve? .
Even Euler’s equation is more beautiful using :
And it even makes sense! What that says is: the complex exponential of turning around a full circle is 1. Which means: if you multiply a complex number by , that’s basically the same thing as treating it as a vector, and rotating it by an angle of
: so what
means is rotating it all the way around the circle: Euler’s equation becomes a very clear statement of the fact that the complex plane is symmetric with respect to that rotation.
It really does make sense. I actually think that he’s right. I think that human inertia is going to make it close to impossible to convince people to change – but I think he’s right, and the correct fundamental circle constant is .

I remember when I first heard about tau, I was kind of a skeptic. But honestly, a lot of formulas look nicer using it. Not that I’m going to start using it in my papers or anything; I think that there’s too much mathematical inertia and precedent for pi.
You are missing a negative sign in the exponent in the second Fourier transform equation.
I saw this recently and was initially skeptical, but only until I read about halfway through the page, now I’m pretty convinced. I was trying to think of formulas that are simpler using pi than tau, and I couldn’t really think of any, especially after seeing the quadratic form explanation for tau/2*r^2. When I saw this blog post, I thought maybe you had some good counterexamples, but I guess not – maybe tau really is right.
I agree that tau is a great idea, but I’d mourn for that old classic:
Area of a circle = pi * r^2
tau/2 * r^2 makes me a sad panda.
except now you can immediately see that the area of a circle is the antiderivative of the function tau*r.
exactly!!!
Because it’s not immediately obvious that pi*r^2 is an antiderivative of 2*pi*r?
Not as immediately obvious, no. Obviously.
I recall a book by A. Eagle called The Eliptic Functions as They Should Be in which the author calls pi over two “ti” and uses something that looks a little like a tau as the symbol, actually half of a printed pi.
Hmm. I think I might get my trig final wrong if I use tau instead of pi in the formulas.
But this makes more sense. I’ve often wondered why we don’t have a symbol for 2π, since π is almost never used without its friend the 2.
I’m gonna be conservative and stick to pi.
Since I mostly work in 3D, i’m seeing a lot of factors 4pi for surface area and volume, these don’t get any simpler if you replace em by 2 tau.
Some of the trig identities become ugly:
cos(x + pi) = -cos(x) etc…
Also, Euler’s formula using tau does not show that there is a form of antisymmetry when you do a half rotation, which I think is just as important.
I’m sure I can think of a few other counterexamples, but I gotta go to work now.
Could you debunk this? http://images.cheezburger.com/completestore/2010/11/24/9e7c48aa-1823-4d5f-aa13-40699c72d508.jpg
You might want to… I don’t know… read other posts on Pi before asking the same thing to be repeated. Also, try doing it yourself. Look at the first iteration, then the second, and see if you see a pattern.
It’s actually been mentioned in another thread here, but the solution is based on the fact that the limiting procedure isn’t correct. When you repeat that process to infinity you don’t actually get a circle but another square with corners rotated 45 degrees. (That is, the dashed diameter shown in the picture runs along one of the square’s diagonals.)
What the picture has really proven — minus the last step, of course, which doesn’t actually follow — is that the perimeter of a square is invariant to rotation. 😛
I don’t think this explanation is correct; the shape generated by the limit of that process isn’t a square. The construction does give a (loose) upper bound for the circumference of the circle — the error is in the implication that the depicted process makes the bound converge in the limit.
In fact, the procedure explained in the cartoon is entirely correct if you use it to compute the area of the disk. You can thus use it to determine pi but through the area formula.
It goes wrong because it is not a correct approximation for the perimeter, you can’t approximate the length of a chord by using the square segments they propose, you need the diagonals of the segments. See in any textbook on integration how the length of a chord is computed by integrals.
Well for one thing, you could play the same game with any regular polygon, which would give you an infinite series of possible values for pi. (The correct value is, of course, the limit of that series.)
That shows that the argument has to be wrong, but doesn’t really explain why it’s wrong. I think that what you wind up with when you repeat the infinite corner-removal process is not actually a circle, but a fractal which somehow has the same shape as a circle. I don’t know enough about fractal geometry to formalize that intuition, though.
There problem with this is that arclength is not a continuous function on the space of plane curves. You can do the same sort of thing to show that sqrt(2)=2 by starting with a 1×1 square and making “staircases” of length 2 that approach the diagonal which has length sqrt(2).
Debunked. Think about it! a square is not a circle! and in the cartoon the square has a diameter of 4 well this just can’t be true the circles diameter is 4 the side of the square is 4 there fore the only conclution you can draw is that diameter = 4 or Length and Width = 4 not Pie = 4 (Now I am Hungry for some reason)
oh yes and area of square is L*W so the area of the square would be 16
not 4 and the area of the circle would be tau/2 * 4 = 12.57
A Problem with this change would be that ins some areas of research, pi is used as the distance between zeros of the sine function. This mainly implies working with Energies because this is also the period of cos^2.
Although now that I think about it we use the first zero of the cosine function ( pi/2 ) more often than the period. So tau = /2 would also make more sense for my area.
One identity that would less elegant using $tau$: $e^{ipi}+1=0$, a compact little equation involving five important mathematical constants
$e^{ipi}+1=0$ becomes $e^{itau}=1+0$, as covered in the link.
Not quite convinced myself either, but I’m curious enough to poke at it and see more of what it does.
Nope, sorry, spoils Euler’s identity. It makes lots more sense in a lot of contexts… but Euler’s identity is far more beautiful if you use
spoils Euler’s identity. It makes lots more sense in a lot of contexts… but Euler’s identity is far more beautiful if you use  .
.
I’ve never understood why it was so important to include 0 in euler’s formula. It always made more sense to me to write , which as mentioned above reflects the antisymmetry when rotating by 180 degrees. The 0 in
, which as mentioned above reflects the antisymmetry when rotating by 180 degrees. The 0 in  is already extraneous, as is the addition.
is already extraneous, as is the addition.
Because zero and one are the additive and multiplicative identities that make Q, R, C, etc. true fields. It’s nice to see all four fundamental constants in a single formula.
Anyway, it’s Euler’s Identity, which is a special case of Euler’s formula: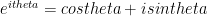
I had the same concern regarding Euler’s Identity, but then this occurred to me: write it as $e^{itauover 2}+1=0$. This is not quite as nice as $e^{ipi}+1=0$, for the reasons that you suggest, but it has its nice qualities, too. 2 is kind of nifty, as it is the only even prime. It also has relevance to numeration systems (especially binary), giving it a nice comp sci link.
That being said, I am inclined to agree that $tau$ spoils the identity. Moreover, I don’t want to go through the trouble of tattoo removal. 😉
I agree completely. The first time I saw this proposition it felt so natural I started thinking in terms of 2pi almost immediately, only reverting to pi when I talk to another.
It also seems more natural to think of radius than diameters.
It is one of those things our intuition tries to tell us but we do not see clearly until someone else tells us.
I didn’t expect so much people to accept it.
Now you can expect a bunch of cranks saying “I told you! Pi is wrong!” XD XD
Not a biggie, but your revised definition of the inverse Fourier transform misses out a – sign in the exponential.
Otherwise, this is something that really annoyed me throughout High School, pretty much all of the maths in analogue electronics would have been so much neater with pi redefined as 2*pi
Even since I read Palais’ article a few years ago, I’ve been a convert. As soon as I need π in a piece of software, I immediately define
constant turn = 2 * pi;
(Palais used “turn” or a three-legged π in his article – I guess now I’ll have to switch to τ)
I still like the three-legged π better. τ has many uses, so I believe it is a bad choice.
Of course, the problem with the three-legged π is that it requires computer support so we can use it.
Nice as the idea may be, I think you have more chance of inventing a new unit of mass that doesn’t have a prefix in its own name already, than of replacing 2 * pi with tav.
Lots of things are wrong, but are so deeply entrenched that it’s easier to live with them than actually to do anything about them.
I basically agree with this, except for one very strong disagreement on this point:
First, a small nitpick: That’s Euler’s identity, not Euler’s equation. But that’s neither here nor there, and not really worth commenting on.
Far more importantly…. I’m sorry, but you are just wrong. The most beautiful expression of Euler’s identity, and the one I have tattooed on my left shoulder, is:
(Arguably) the five most fundamental constants in mathematics, each appearing exactly once, connected by (arguably) the four most fundamental operators in mathematics, each also appearing exactly once. Your “more beautiful” formulation does not contain zero, nor any additive operations. Which makes it less beautiful in my book.
Other than that, though, there seems to be a good case for .
.
I completely agree. I have Euler’s proof of the infinitude of primes tattooed on my thigh. Now I have to think about that one too.
I don’t have it tattooed on me (although that is highly tempting, and just might work better for me than finding the ideal frog), but I made a box using plastic canvas & needlepoint on it before assembling the bits as a box, and the bottom has that form of Euler’s identity, and there’s still a little piece of my 16-year-old self that will cry if we switch to tau for everything.
(An odd little geek I was, yes.)
e^{itau} – 1 = 0
Do you have any good reason to prefer addition over subtraction?
I like this, though there have been a few counter-examples where pi still works better.
That said, it’s not like tau would eliminate pi completely. It could be used where it works cleaner and pi would still be around for those situations where it works cleaner. In fact that’s probably what the natural curve of adoption would look like anyway.
So one thing that occurs to me… is the only fundamental constant that comes to mind where it is still equally fundamental if you linearly scale it by an integer (within reason…
is the only fundamental constant that comes to mind where it is still equally fundamental if you linearly scale it by an integer (within reason…  makes sense, and
makes sense, and  has some clear utility, and I could even see an argument for
has some clear utility, and I could even see an argument for  … but
… but  ain’t so fundamental) (well, I suppose technically you could say the same thing about zero, but only trivially so).
ain’t so fundamental) (well, I suppose technically you could say the same thing about zero, but only trivially so).
1? Not even close!
I’m not really familiar enough with other famous constants to say. And I’m not sure this means anything. But it’s interesting… you can have a vs.
vs.  argument, but you can’t have a
argument, but you can’t have a  vs.
vs.  argument! (Would you call it
argument! (Would you call it  ?)
?)
I know it’s not a linear multiple, but I think that the reciprocal of the golden ratio, known as the golden ratio conjugate, is just as fundamental as the golden ratio itself. I can’t think of any application of the golden ratio where the golden ratio conjugate wouldn’t do just as well.
There’s at least two completely different reasons why that’s correct.
I’m going to have to disagree about integer multiples of 1 not being fundamental. To make this claim, you’d have to support the idea that integers themselves are not fundamental!
While we’re changing poor choices of syntax, can we fix current so that it matches electron flow? And all the other bad notation that has accumulated over history?
Btw, complexity theorist R. J. Lipton wrote a great blog last week on the importance of notation (https://rjlipton.wordpress.com/2010/11/30/notation-and-thinking/). He mentions the movement, as well as some other compelling examples of both good and bad notation.
movement, as well as some other compelling examples of both good and bad notation.
As an electrical engineer, I’m not sure I agree with that.
http://amasci.com/miscon/eleca.html#frkel
An interesting “one-up” suggestion that I think is due to Terry Tao is that an even better constant would be (2pi i); note that this expression appears together in *each* of the equations in the OP.
I have similar information theoretic arguments for replacing hbar (Planck’s constant over 2pi) with hbar/(2pi) (Planck’s constant over 4pi^2). I dont’ think I’ll ever try to convince the community, though.
This was worth it just for the headline.
I’m wondering if the process algebra known as π-calculus should become τ/2-calculus then 😉
More seriously, 2s are there quite often but not always (as stated already), which kind of defeats the main purpose…
I like this idea quite a bit, even though I do prefer (as several others have mentioned) the e^ipi+1=0 form of Euler’s equation.
Regardless, I think it would be far more important to change the notation of inverse trig functions so I and many others can stop explaining to students why sin^-1x isn’t equal to cscx.
I was pretty sure we already had arcsine for that.
Yeah, we do. We have 3 notations for 2 ideas, the most confusing of which appears in a lot of textbooks and on every calculator I’ve ever seen.
I think that being able to understand that sin^-1=/=csc should definitely be a prerequisite for a good grade. Especially when in later years you encounter something like (3,19) and you’re supposed to be able to deductively figure out if that refers to an interval, and ordered pair, gcd, etc.
Pi is the wrong constant because the formula A = pi R squared is wrong, since everyone knows pi R round. The correct constant to use is brownie since obviously brownie R squared.
It’s been long obvious to mathematicians that the fundamental number here is the period of the zero-genus curve (aka, a conic; over ℂ, it is birationally equivalent to a circle). In the same way, 4K and 4iK’ are two generators of the lattice of periods of a complex elliptic curve (with the fours being precisely as useless as the two for the circle), and the period of the Jacobi elliptic functions sn, cn and dn. Think of the period(s) as the integral(s) of an invariant differential (ω = dθ = (x·dy – y·dx)/(x²+y²) in the case of the circle) along closed curves generating the homology of our curve (in the circle case, the circle itself).
The argument about the translation formulas for f(t+π) is not serious anyway, since all those formulas are best understood through the quarter-period (that is, π/2) translation matrix, which is simply a quarter-turn rotation, or multiplication by i. The formulas for half-period translation are then deducible simply by squaring this matrix (or squaring i, which obviously gives -1).
I’m sorry, but the correct constant is in fact τ=π/2. This was shown by Albert Eagle Elliptic Functions as They Should Be (Galloway & Porter, Cambridge, 1958).
This certainly makes more sense logically: one leg is half as many as two legs. Eagle also recommended that the “tau” be pronounced “hi”. More technically, “hi” is the amount of argument change that turns sine into cosine and vice versa, and thus it corresponds to the K that turns (elliptic) sn into cn and vice versa.
Eagle made numerous other recommendations, but this is the one that’s been burned in my memory for thirty years now. The book really is a masterpiece in exposition regarding the inner meaning of elliptic functions, and does far better than anyone else in imposing a logical order to the haphazard notation that usually makes the subject matter cruelly confusing. Unfortunately, the world is still not ready for all of his notational changes. (For example, he would also write 1/2stuff meaning (1/2)stuff and similar shortcuts that you can get away with if everything else is absolutely clear. But of course, one rarely is in that ideal position in real-world mathematical reading.)
I dug up my copy of Eagle, and found some more of his other notational suggestions. In a few cases, he seems to have caught the start of a trend. In others, he is still all by himself.
One point he makes is that one very frequently integrates from 0 to π/2 or 0 to τ in his notation. As he says, this would be read “from nought to hi”, as in “hi”=”high”=”upper end”. (I note this gets typeset with the wrong quotation marks.)
He of course uses the British convention that a baseline period means multiplication (and is not the decimal point). He uses an extra bold face (Clarendon) period to mean binding weaker than addition. For example, 3+4⋅5+6=29 but 3+4•5+6=77 (where I’m using centered dots since that’s what HTML gives me). His goal is to use fewer parentheses in complicated expressions.
He writes !5 instead of 5!—not just because that is proper function notation but because we say “factorial 5” instead of “5 factorial”. (I have no idea if this is a generation thing or a British thing—as an American born after his book was published, I’ve only heard “5 factorial”.) He does not bother with the Γ function.
He complains about the “cosec” function, which for him is “csc”. He complains about “arc sin” or “arg cosh” functions, and uses “sin-1” and “cosh-1”. (Well, I put in sup tags, but they didn’t take.) I suspect this changeover really happened because of calculators.
As for the suggested symbols for 2π, both tau and the triple-leg pi are not really good choices. But it seems the very rarely seen $varpi$ (the variant pi that looks like a lower-case omega with a tilde welded on top) is ideal. It’s triple-legged, it’s easily typeset, and it’s not being used for anything important anyway.
If the astronomers can all get together and demote Pluto, the mathematicians can certainly all get together and demote pi.
You forge your will in the crucible of your mind, Mark (or something something). Pick up the torch! Carry on!
I believe that pi will die within a generation or two (one or two turns of the wheel).
I also believe that when we meet our first extra-terrestrials that are open to discussing mathematics, they will naturally use 6.28. Because it is natural.
More interesting will be what base their counting system uses? i.e. do they have ten fingers and ten toes like we do?
Like so many Americans, these mathematicians only want to do things halfway. Furthermore, you still can’t get Tau without using Pi, so there.
I basically not agree with this, except for one very strong disagreement on this point:
Area of a circle = pi * r^2 and circumference of circle = 2pi*r
After using TAU
Area of a circle = tau/2 * r^2 and circumference of circle = tau*r
No relation between pie and tau.
Just curious whether any of you guys with pi or tau tattoos have any trouble getting dates. heh
I’m happily married with two kids. So obviously, no, didn’t have a problem there.
Fwiw, were my better half to ever get a tattoo, tau would top his list of options. It’s part of his charm and why I married him.
Btw, thanks for the inspiration source for my new username; it works on so many levels. Anon commentors are typically circuitous and holier than thou…
“Angular frequency”, ω = 2π*f, is in actually used quite a bit. Where f=frequency and is usually in units of 1/[seconds].
So, instead of putting 2π*f in a formula they just put ω. Usually, f is a frequency or rotation per second. Then ω is radians per second; 2π for one rotation. For example ω is used in e^iωt or sin ωt. So, in rotations ω, is the rotational speed (angle) in radians per second.
It is used often in the math of mechanical rotations, oscillations, differential equations, and Fourier analysis.
The same people who use ω also use τ=1/ω=1/(2πf). This is known as “time constant”. An example would be, e^(t/τ).
One can google “angular frequency” and “time constant”. There is also an angular acceleration, .
This method replaces three symbols with one. This practice validates you idea.
ω omega
π pi
τ tau
@ whoever said that tau spoils Euler’s equation, it doesn’t. e^i*tau = 1 does not at first appear to have addition or 0 in it until you do this…
e^(i*tau) = 1 + 0
and the person who said the 0 is extraneous, it isn’t, because it is naturally there from the equation e^ix = cos(x) + isin(x), and isin(tau) happens to be zero. So there. Sorry, tau in fact does not spoil Euler’s identity.
And btw, before e was popularized as the base of the natural log, some people defended the use of 1/e instead, so I guess pi isn’t the only controversial constant.
I do completely agree that tau is more fundemental than pi and we should definitely switch. After all, most of the world has converted to the metric system and I’m sure this won’t be any harder. I’m telling every mathsy person I know about this and to convert. So far everybody I’ve talked to tau about agrees that it is more fundemental, and all but one person (my teacher) thinks it’s worth changing. I’m officially converting to tau. I’m only going to use pi when doing school homework.
@Euler’s identity…
2 is missing in there! It’s the smallest integer you can build a number system on (binary,…, decimal,…, hexadecimal).
And upon mathematical beauty: tau is (approximately) 6.28, right?
Well, 6 and 28 are the first two perfect numbers!
Pingback: Friday Links (17-Dec-10) | Fail Blue Dot