The comment thread from my last Cantor crankery post has continued in a way that demonstrates a common issue when dealing with bad math, so I thought it was worth taking the discussion and promoting it to a proper top-level post.
The defender of the Cantor crankery tried to show what he alleged to be the problem with Cantor, by presenting a simple proof:
If we have a unit line, then this line will have an infinite number of points in it. Some of these points will be an irrational distance away from the origin and some will be a rational distance away from the origin.
Premise 1.
To have more irrational points on this line than rational points (plus 1), it is necessary to have at least two irrational points on the line so that there exists no rational point between them.
Premise 2.
It is not possible to have two irrational points on a line so that no rational point exists between them.
Conclusion.
It is not possible to have more irrational points on a line than rational points (plus 1).
This contradicts Cantor’s conclusion, so Cantor must have made a mistake in his reasoning.
(I’ve done a bit of formatting of this to make it look cleaner, but I have not changed any of the content.)
This is not a valid proof. It looks nice on the surface – it intuitively feels right. But it’s not. Why?
Because math isn’t intuition. Math is a formal system. When we’re talking about Cantor’s diagonalization, we’re working in the formal system of set theory. In most modern math, we’re specifically working in the formal system of Zermelo-Fraenkel (ZF) set theory. And that “proof” relies on two premises, which are not correct in ZF set theory. I pointed this out in verbose detail, to which the commenter responded:
I can understand your desire for a proof to be in ZFC, Peano arithmetic and FOPL, it is a good methodology but not the only one, and I am certain that it is not a perfect one. You are not doing yourself any favors if you let any methodology trump understanding. For me it is far more important to understand a proof, than to just know it “works” under some methodology that simply manipulates symbols.
This is the point I really wanted to get to here. It’s a form of complaint that I’ve seen over and over again – not just in the Cantor crankery, but in nearly all of the math posts.
There’s a common belief among crackpots of various sorts that scientists and mathematicians use symbols and formalisms just because we like them, or because we want to obscure things and make simple things seem complicated, so that we’ll look smart.
That’s just not the case. We use formalisms and notation because they are absolutely essential. We can’t do math without the formalisms; we could do it without the notation, but the notation makes things clearer than natural language prose.
The reason for all of that is because we want to be correct.
If we’re working with a definition that contains any vagueness – even the most subtle unintentional kind (or, actually, especially the most subtle unintentional kind!) – then we can easily produce nonsense. There’s a simple “proof” that we’ve discussed before that shows that 0 is equal to 1. It looks correct when you read it. But it contains a subtle error. If we weren’t being careful and formal, that kind of mistake can easily creep in – and once you allow one, single, innocuous looking error into a proof, the entire proof falls apart. The reason for all the formalism and all the notation is to give us a way to unambiguously, precisely state exactly what we mean. The reason that we insist of detailed logical step-by-step proofs is because that’s the only way to make sure that we aren’t introducing errors.
We can’t rely on intuition, because our intuition is frequently not correct. That’s why we use logic. We can’t rely on informal statements, because informal statements lack precision: they can mean many different things, some of which are true, and some of which are not.
In the case of Cantor’s diagonalization, when we’re being carefully precise, we’re not talking about the size of things: we’re talking about the cardinality of sets. That’s an important distinction, because “size” can mean many different things. Cardinality means one, very precise thing.
Similarly, we’re talking about the cardinality of the set of real numbers compared to the cardinality of the set of natural numbers. When I say that, I’m not just hand-waving the real numbers: the real numbers means something very specific: it’s the unique complete totally ordered field 
I’m not just saying that to be pedantic. I’m saying that because we need to know exactly what we’re talking about. It’s very easy to put together an informal definition of the real numbers that’s different from the proper mathematical set of real numbers. For example, you can define a number system consisting of the set of all numbers that can be generated by a finite, non-terminating computer program. Intuitively, it might seem like that’s just another way of describing the real numbers – but it describes a very different set.
Beyond just definitions, we insist on using formal symbolic logic for a similar reason. If we can reduce the argument to symbolic reasoning, then we’ve abstracted away anything that could bias or deceive us. The symbolic logic makes every statement absolutely precise, and every reasoning step pure, precise, and unbiased.
So what’s wrong with the “proof” above? It’s got two premises. Let’s just look at the first one: “To have more irrational points on this line than rational points (plus 1), it is necessary to have at least two irrational points on the line so that there exists no rational point between them.”.
If this statement is true, then Cantor’s proof must be wrong. But is this statement true? The commenter’s argument is that it’s obviously intuitively true.
If we weren’t doing math, that might be OK. But this is math. We can’t just rely on our intuition, because we know that our intuition is often wrong. So we need to ask: can you prove that that’s true?
And how do you prove something like that? Well, you start with the basic rules of your proof system. In a discussion of a set theory proof, that means ZF set theory and first order predicate logic. Then you add in the definitions you need to talk about the objects you’re interested in: so Peano arithmetic, rational numbers, real number theory, and the definition of irrational numbers in real number theory. That gives you a formal system that you can use to talk about the sets of real numbers, rational numbers, and natural numbers.
The problem for our commenter is that you can’t prove that premise using ZF logic, FOPL, and real number theory. It’s not true. It’s based on a faulty understanding of the behavior of infinite sets. It’s taking an assumption that comes from our intuition, which seems reasonable, but which isn’t actually true within the formal system o mathematics.
In particular, it’s trying to say that in set theory, the cardinality of the set of real numbers is equal to the cardinality of the set of natural numbers – but doing so by saying “Ah, Why are you worrying about that set theory nonsense? Sure, it would be nice to prove this statement about set theory using set theory, but you’re just being picky on insisting that.”
Once you really see it in these terms, it’s an absurd statement. It’s equivalent to something as ridiculous as saying that you don’t need to modify verbs by conjugating them when you speak english, because in Chinese, the spoken words don’t change for conjugation.
Okay, using my intuition (which of course you just told me I shouldn’t do, but alas I am not conversant with ZFC. etc.) if I take the infinite decimal representation of any two non-equal irrational numbers, I can always truncate them and then form an infinite number of rational numbers that are between them. And on the same token, given any two non-equal rational numbers, I can always form an infinite number of irrationals between them. This is in accord with his premise 2 in the proof above. But it also shows why his premise 1 is false, but not a requirement since if there are an infinite number of rational and irrationals between any two points, their cardinality might be different. Which is just another way of saying that premise 1 is false and Cantor is still right.
I’m not sure Premise 2 is right either. Consider two real numbers whose decimal representations are the concatenation of two infinite sequences where the first sequence is the same between them but the second is different. For instance, n1=0.000…001111… (an infinite sequence of 0s followed by an infinite sequence of 1s) and n2=0.000…002222… (an infinite sequence of 0s followed by an infinite sequence of 2s). Any finite trucation of these two numbers will yield the same number, with no room for any numbers between them. In fact, I can’t think of any rational numbers that would fit between their non-trucated forms. Yet, they are clearly not equal.
I’m pretty sure both of the premises are wrong; but identifying any error in a premise is enough to trash the entire proof, so I stopped there.
>I’m pretty sure both of the premises are wrong
The second premise is rather boringly true; between any two (distinct) real numbers, you can find a rational.
Premise 2 is true (and, indeed, proving it is a standard exercise in first-year university analysis courses): since I just finished marking a bunch of bad proofs of it, here’s a better one (using your definition of real numbers):
Given any two real numbers a and b, if a =/= b, then WLOG, a > b (otherwise, just swap a and b over). Therefore, a – b > 0. Since the sequence (1/2^n) convergest to 0 and is positive for all n, there is some N such that 0 < 1/2^N < (a – b). Now, there are integers c and d such that c/2^N a (the former since (-n/2^N) tends to minus infinity as n tends to infinity, and the latter since (n/2^N) tends to infinity as n tends to infinity). Obviously, d > c, so the set of integers c such that c/2^N b (else c* would not be maximal), and (c* + 1)/2^N = c*/2^N + 1/2^N < b + 1/2^N < b + (a – b) = a, so b < (c^* + 1)/2^N < a, and (c^* + 1)/2^N is rational since both 2^N and c^* + 1 are integers.
I don’t believe it’s valid to concatenate infinite sequences. Doesn’t “followed by” actually mean “comes after the last element of the previous sequence”? If a sequence doesn’t have a last element, then nothing can come after it.
I’d argue that it’s not even wrong.
That is, “concatenate” isn’t a meaningful term when you’re talking about infinite sets. There are so many different ways that you could define it. There are some definitions of concatenate in which it would make sense and be true; there are some definitions of concatenate in which it would make sense and be false; and there are some definitions in which it just doesn’t make any sense.
That’s exactly the point I was trying to make. In math, we don’t use undefined terms. If we wanted to use the word concatenate, we’d give it a specific formal definition which identified what we mean, instead of just using the natural language work and relying on intuition to fill in the meaning.
Sure, “concatenate” has meaning for infinite sequences. The problem is decimal notation requires a sequence of order type at most ω, but red is offering sequences of order type ω+ω!
Premise 2 is indeed wrong, and it’s a fun little recreational mathematics exercise to prove this.
Hint: Use continued fractions.
Wait, no, the double negative in the premise threw me. The premise is correct. Given any two distinct irrational numbers, it is possible to construct a rational number between them.
The problem with red’s argument is that 0.”an infinite sequence of 0s followed by an infinite sequence of 1s” is not a decimal numeral.
A decimal expansion is only infinitely long. It doesn’t make sense to talk about “numbers whose decimal representations are the concatenation of two infinite sequences,” because you have to stop after the first infinite sequence. This is a property of the definition of decimal expansions.
And Premise 2 is correct; it’s simply saying that the rationals are dense in the reals, which is true.
For precision, it’s worth pointing out that you can, in the right model, with the right definition of “concatenation”, talk about something like the concatenation of two infinite sequences.
The problem is, he’s using the informal word “concatenation” in a way that doesn’t make any sense in the system that he’s talking about. You can’t “concatenate” two infinite decimal expansions and get the properties that he thinks he’s getting.
In the formal definition of real numbers mentioned in the post, your n1 and n2 are not real numbers.
Neither n1 nor n2 is a real number. Premise 2 is entirely correct.
Hi MarkCC, I’ve meaning to ask you for your views about the learning resource https://betterexplained.com, as the emphasis there is providing “intuitive” learning guides to mathematics. From reading this article, I assume you’re against such teaching methods, no?
I haven’t looked at their site, so I’m talking in the abstract here.
My point isn’t that intuition is useless; it’s that you need to be able to understand the limits of intuition.
When I was in high school, I was an honors math student; my older brother, who was a musician, was in the “normal” math classes.
He was taught strictly rote. He’s a very smart guy, but coming out of those math classes, he had no idea what something like “percent” means. To figure out what a 20% off sale price was, he’d write down a pair of ratios, cross-multiple, and solve. The process didn’t mean anything to him.
I consider that to be an absolutely criminal failure of the normal math classes. They taught procedures and memorization without any reason behind it – and that meant that their students had absolutely no concept of what any of it meant – which means that they might as well not have spent time learning any of it at all, because it was just meaningless procedures.
You need to understand what things mean. In elementary math, that means that it’s absolutely essential to teach intuition. But as you get further and further along into deeper math, you reach a point where you have to accept that your intuition has limits, and that while intuition is a useful tool for understanding things, you can’t rely on it.
I’ve always felt the point of doing proofs in a ln area of maths was to *build* the correct intuitive understanding of that area.
“…which means that they might as well not have spent time learning any of it at all, because it was just meaningless procedures.”
Not a very convincing statement, considering you preceded it by stating that your brother can calculate useful results.
I get what you mean, but generally speaking mathematicians undervalue the worth of simply being able to calculate useful results even without understanding why the algorithms they apply work.
He could produce a useful result, but in an impractical way, without understanding how or why it worked. That’s not actually useful. Knowing how to set up parallel ratios and cross multiply doesn’t do you much good in practice in the real situations where you encounter discounts.
Nice detail. I probably would have said, “Let’s put aside Cantor’s argument for a moment. How do you think the cardinality of the natural numbers compares to that of the even natural numbers.” My guess is that the person would intuit that there are “fewer” even numbers without distinguishing between the notions of cardinality and proper subsets. It may be an easier context in which to make your point about the need for formalism.
I once had a similar experience with a person who claimed that the product of two negative numbers “should” be negative because that “makes sense”.
And my comment is rendered moot by your previous post on this topic, which I neglected to read first. Sorry about that.
If avoiding small errors so so important, I wonder how mathematicians can be confident in their proofs without any computer checking. I’m pretty sure I couldn’t write a complicated program that works without a compiler and lots of testing, and even then there are bugs.
But what seems to happen in practice (I’m told) is that mathematicians can work entirely on paper, skipping most of the formalism, while still being able to generate it on demand. And somehow, small errors in proofs usually don’t turn out to be fatal – they can be patched.
It all seems rather mysterious. Formalism is very important in theory, but somehow not in practice once you get beyond high school geometry?
This reminds me of my undergraduate days, being asked to prove things without a clear sense of what the rules actually are. It’s not like they’re all written down in a big book that you can refer to. The whole thing seemed suspiciously *in*formal from a computer programmer’s perspective.
Being able to formalise is important; you can’t spot the mistakes if you can’t formalise your proof. The thing about experienced mathematicians is that they’ve trained their intuition such that the things they intuit tend to match up to the things that they can formalise; this, in turn lets them skip the formalism during the exploratory phase of proving something, and lets them add it in at the end.
In my experience, you train on valid proofs and counter-examples until you build a good intuition for that area. Of the two maths areas I know best – differential geometry and logic – the first is much more amenable to intuition than the second.
Actually, no, the papers written by mathematicians contain plenty of formalism. If any formalism is omitted, it is merely that of some minor bits that have been addressed before many times, and so these minor bits are used freely, just like previously proven theorems are used without replication of the proofs. Mathematical papers tend to introduce new definitions and new notations, and these are done very formally in order to avoid errors.
For example, any paper dealing with real numbers will assume that the real numbers are the smallest complete ordered field containing the field of rational numbers, where the notion of “complete” has already been defined in the mathematical community. This notion of completeness has various equivalent forms (equivalent because we have proven them so): Axiom of Completeness, Nested Interval Principle, Bolzano-Weierstrass Theorem, etc. The equivalence of these is established in an undergraduate course in Analysis. So the author will use notions of completeness, convergence, and other concepts freely. If the author introduces some new property called “foo sets” of real numbers, then they will be required to very formally define a “foo set”.
Regarding the checking of proofs, this is done by peer review, and any result of great interest will be checked by far more people than merely the journal-assigned referees. Computer-checking is far from fool-proof, and mathematicians have been wary of the use of computers in proofs. Computers must be programmed by fallible humans, and computers have limitations. The concern for mathematicans is whether a human checked the computer! And when a lot of computer work has been done, say in a proof of The Four Color Theorem, some people regard the proof as not really legitimate and continue to seek a traditional proof. Some of this skepticism has relaxed, but it has raised a new issue of requiring computer-assisted proofs to be open-source so that there can still be a peer review.
I remain somewhat skeptical. It’s apparently not uncommon for mathematical texts to have minor errors that that experienced readers just gloss over (because they know what was actually meant) but trip up the uninitiated. Also, mathematical notation can be idiosyncratic and sometimes ambiguous. I’ve also read that making mathematical proofs fully computer-checkable is very tedious, which makes me a bit suspicious. If it were fully formalized in a consistent language, it seems like it shouldn’t be that hard?
Completely agree that for static analysis tools to be fully trusted, they should be open source, and perhaps have multiple independent implementations.
I’m not sure it’s necessary though. Just like you can use a spell-checker to find some errors even if you don’t fully trust it on spelling (or for finding any other kind of writing error), it’s possible to use a static analysis tool that sometimes has false positives or false negatives, or is incomplete. And we do that all the time in computer programming with linters.
This is similar to how we don’t expect perfection from any single *human* reviewer. Holding static analysis tools to that standard seems a bit unfair.
I don’t entirely disagree with you.
Unambiguous notation is an aspiration, and all too often, we fail to achieve it.
But even when we do, the problem is often more the fact that we omit things when we present them to other people, and those omissions cause all sorts of problems.
In terms of automated proof systems, I think that there’s a significant issue of syntax.
Our mathematical notation is mostly based on handwriting. It’s built to be easy for a human holding a pen to sketch out – not for a computer to process.
For the most part, latex has become a sort of primary language for many people – but it’s geared towards producing something that looks like the carefully handwritten stuff.
I’ve had the misfortune of learning a lot about the internals of TeX (a big part of how I worked my way through grad school was technical support for TeX in the CS and EE departments), and I think it’s difficult or even impossible to extract an unambiguous semantic form. I think that it’s equivalent to just getting the output, scanning it, and trying to parse out the notation in the scanned document. (TeX is a particularly ugly Turing complete computing system under the covers.)
Wouldn’t such a system run afoul of the incompleteness theorem?
Checking a proof to see if each step was a valid application of an inference rule in the logic would not run afoul of incompleteness.
The point of incompleteness is that there are some statements that cannot be proven. That’s fine – if they can’t be proven, then there are no proofs of them.
But if you’ve already got a valid proof, then the thing you’re looking at doesn’t fall under incompleteness.
But if you create a system that is sufficiently unambiguous and self-consistent for a machine to check its validity, you will create a system that cannot prove things that are true. I wonder if you might not want to leave a bit of “wiggle room” to prevent that. This begs the question, can we “get around” the incompleteness theorem to some extent by intuition? Or is the human mind of necessity part of the system?
Static analysis tools don’t need to check everything. All you need is some kind of “this step is not checkable by tool X” annotation. This should get the attention of human reviewers who can review that step more carefully.
blu28, you do not understand Gödel’s theorem. Also, pay attention to the word “some”. There will always be “some” statements in a consistent system that contains Peano arithmetic that cannot be proven true or false. That doesn’t mean you can never prove anything.
I certainly never claimed that you couldn’t prove anything with such a system. Nor do I think it wouldn’t be useful to work towards such a system.
There’s a neat trick you can pull off in a static analysis system to get the “not checkable” thing to work; you require the “not checkable” step to become an axiom.
You can then extract the axioms from the proof, and examine them more closely; mostly, they’ll be standard axioms, and the system simply tells you that all statements its verified are true given these axioms from the standard libraries, plus these assertions made in the proof that cannot be checked.
The proof user then looks at the axioms and the assertions, and confirms that they’re happy with that set – if they’re not happy, then they know what hypotheses need to be proved within their acceptable set of axioms to get the proof to hold.
“I remain somewhat skeptical. It’s apparently not uncommon for mathematical texts to have minor errors that that experienced readers just gloss over (because they know what was actually meant) but trip up the uninitiated.”
You just pulled a switcheroo. Do you want to talk about mathematical textbooks or mathematical papers? Choose one. Mathematical textbooks are not representative of mathematical papers. (Actually, in most disciplines textbooks and papers are written very differently.) Mathematical papers are not for the uninitiated.
Also, remember that mathematical papers cite references. It is common for an author to cite a textbook and direct the reader there for some definitions and notation, so they can rest on the formalism of another work rather than duplicate it. Their new contribution, however, will be done formally.
I think that it would very good to see the proof that convinced MarkCC that Cantor’s diagonal argument is indeed true. So Mark, if you don’t mind, would you provide a link to such a proof?
The proof that convinced me Cantor’s diagonal is true is… Cantor’s diagonal. Shocking, huh?
It’s a very simple proof, each step of which is well-founded by the axioms of ZF/FOPL + Peano arithmetic and real number theory.
It’s been written thousands of times in thousands of different forms, including an informal presentation several times right here on this blog.
If you actually care (which I’m pretty sure you don’t), get a good textbook. I’ve got https://www.amazon.com/Set-Theory-Its-Logic-Revised/dp/0674802071/ref=sr_1_8?ie=UTF8&qid=1473546149&sr=8-8&keywords=axiomatic+set+theory, which isn’t the easiest presentation, but it’s quite thorough, and reasonably clear for a formal text.
Here is a book which discusses Cantor’s argument, but also includes another proof of the result using the nested interval principle, which is nice because the proof does not have to explain the decimal representation aspect. I chose this text for the introductory real analysis course I teach every Fall.
https://www.amazon.com/Understanding-Analysis-Undergraduate-Texts-Mathematics/dp/1493927116
I now have the book, “Set Theory and Its Logic”, but I am having difficulty finding the formal proof of Cantor’s diagonal argument. Can you tell me which page it is on?
I find it interesting that Mark pays lip service to “formal proofs”, yet when I ask him for the the formal proof that convinced him that Cantor’s diagonal argument is valid, I get nothing, except perhaps a book and a wild goose chase.
I think that what happens is that these professors get a hold of gullible students and once indoctrinated, the students will never look at these theories with any skepticism at all.
Below, is a good example, the argument proposed by this UC Davis professor can’t be valid, because it requires the number in the ith place of the ith row to be changed into a number that is not a 0,1,9 or the original number. So, the proof will work only in base 5 or higher. So, unlistability may just be a property of base 5 or larger numbers and not of the set real numbers at all, but these students will go on thinking that Cantor’s diagonal is valid, just like Mark did.
A “wild goose chase” is referring you to the most well-known canonical textbook on set theory.
But your half-assed informal statements? Those we should just take at face value, right?
Yeah. Sure.
Mr. McClain must be clairvoyant, as he posted a very relevant reply to this new rant a couple of months ago, referring to a very well known proof that does not use decimal representation. You can also find it in lots of books, like Terry Tao’s. But it is good to remember that there are several ways of proving Cantor’s theorem. It is funny, by the way.
Let me point out a couple of big problems with your argument here.
To begin with, with this latest thing, all that you’re doing is showing that you really don’t understand number theory – which is pretty damned important, since you’re trying to talk about proofs in number theory. In particular, you don’t seem to understand that numbers exist independent of representation. If Cantor’s proof works for any representation of the set of real numbers, then it’s valid. If the diagonalization only worked on numbers represented in canonical infinite Egyptian fraction form, that would be fine. It wouldn’t matter if Cantor had needed to build a whole new representation that’s only used in the proof – if there’s one representation in which it works, and that representation can be shown to be a valid way of representing the set of real numbers, then the proof is valid.
This isn’t just an abstract point. If you go and read Gödel’s proof of incompleteness, he produces a whole new representation of logic using natural numbers, called Gödel numbering. To make the proof work, you have to convert all of your logical statements into Gödel’s numeric representation of first order predicate logic. But you can’t say that that means that Gödel’s proof only applies to logical statements written using Gödel numbering. Gödel showed that his numeric representation was a valid representation for the set of all statements in FOPL, and so it remains proven and true, no matter what representation you use.
Second, you don’t seem to understand what you’re trying to do here. The burden of proof isn’t on me to satisfy you. You’re trying to overturn one of the most foundational proofs of modern mathematics. It’s been taught to, literally, millions of students over the last century. Every mathematician in the world has studied it.
You’re trying to say that it’s always been wrong, and that every mathematician who’s studied it somehow missed the obvious fact that it’s incorrect.
That’s not impossible. But it is very unlikely. And so, we fall back to that old saw: extraordinary claims require extraordinary evidence.
You’re making an extraordinary claim here. And you’re acting like the default assumption should be that you’re right, and it’s everyone else’s job to prove that you’re wrong.
Sorry, guy, but that’s not how it works. You’re making extraordinary claims, and so it’s incumbent on you to show that your claims are correct. But all that you’ve got backing up your claims is a bunch of logically invalid “proofs”. Commenters here have patiently explained to you what’s wrong with them. Instead of trying to fix the problems, you’re just throwing a little tantrum because no one is giving you everything that you demand.
You want to see a complete, meticulously annotated proof of Cantor’s diagonalization? Get a textbook and set theory, and read it. If you want to claim that you’re a big enough genius to overthrow more than a century of work by the best mathematical minds in the world, you can look up the proof that you claim to have refuted in a textbook.
Years ago, I was talking with a friend about the nature of mathematics and how we personally view mathematics. I was tending towards more intuitive approach, not really believing the intuition but still being more guided by it. My friend was more formal, thinking of symbolic games, etc. Somehow, I explained, that regardless of whether I really thought it to be true, there was a part of me that wanted the math to point to a grander design, a truth behind truths.
We also were talking about The Marshmallow Test in psychology. When some abstract idea is becoming something that you can deal with in your brain, it is important to let it build until it is ready. If you try to grasp it too soon, it may slip out of your fringers. I think whenever I was talking with my friend he was so much more able to let things be until all the required parts were in to make something.
He has a lot more higher IQ than I do. It is just a fact and it shows. He is also one of the most pleasant people to talk about anything as he is able to put himself in the background and be your intelligence when you try to figure something out. Makes me smarter too! Now that is amazing.
Premise 1 even seems to be fallacious even if you ignore the problem of lack of formalism. Why would you assume that infinite things have the same properties as finite things? This is a false equivocation. Hilbert’s Hotel is a simple enough argument even without formalism to dismiss premise 1 as unwarranted. (I know others pointed out issues with the premises, but I felt this one was different enough to warrant posting.)
One of the motivations for developing homotopy type theory was the observation by Vladimir Vodoevsky of mistakes he had made in his own work. He wanted a new foundation to make computerised checking of proofs easier.
And there are currently problems with the foundations of symplectic geometry becauase some of the pivotal foundational papers have been found to contain errors. (Symplectic geometers have been suspicious for a while, and have reorganised the subject to minimise the damage).
So you don’t have to be a crankto get informal mathematics wrong. But the damage to mathemetics is greatest if you are a Fields medalist.
Lovely post, Mark. I know it is a while since the last comment here, but I think that you omitted a crucial detail in your article, which I want to bring to your attention.
Let me start by stating that I completely accept that the diagonal proof does indeed prove that there can be no enumeration of the real numbers in the same language as those real numbers.
Formalized versions of the diagonal argument only establish that, given an enumeration of real numbers, and which is not an enumeration of all real numbers, then another real number can be defined in terms of that enumeration. From this we can further conclude that there cannot be an enumeration of all real numbers, since then we would have a number that was both in and not in the enumeration. That’s all the diagonal proof proves. It says nothing at all about whether there are “more” real numbers than natural numbers. That is given by an additional argument, which is usually not even stated.
Of course, in a correctly formulated fully formal proof, it must be the case that the function that is assumed to exist and which maps the natural numbers to the real numbers must necessarily be in the same language as the real numbers of the proof. Clearly, if an enumeration of real numbers is defined in the same language system as those real numbers, then it is a straightforward matter to define a diagonal number in terms of that enumeration within that same language system.
What you overlook, in common with almost everyone else, is that the argument that the reals constitute some sort of “bigger” infinity arise from an informal argument which is never given in a formal fashion, but which involves different levels of language. It is typically stated like this:
If every real number could be expressed in some language as some finite combination of symbols, then we could easily have a method of matching the natural numbers to these combinations of symbols. All that is required is an alphabetical style ordering of all the symbols used to define real numbers (in the same way as a, b, c … is the order for the English alphabet), and then you simply list them in the same way as you would order the words in a dictionary. And if you could list them, you can obviously attach natural numbers to every item in the list. But this would contradict the diagonal argument, so there must be real numbers that cannot have any finite representation.
Now, that informal argument forces any enumeration of the reals to be in a different language system (a meta-language) from the real numbers of the enumeration (which are in the object language). In short, that informal argument introduces different levels of language while at the same time, using intuition to completely ignore whether that introduction of different levels of language might affect the overall proof.
But in order to prove that a diagonal number can be defined from any infinite such enumeration, it would be necessary to prove that the meta-language in which the enumeration is defined can determine the numerical value of every symbol sequence within the object language that represents a real number – since without that capability, it is impossible for the meta-language to define a diagonal number.
If you can provide such a proof, as you say, “without any vagueness” – perhaps with (as you state in your article) a “notation [that] makes things clearer than natural language prose”, and that does not (as you say) “rely on intuition”, I would very much like to see it. Of course you are aware that in a proof, the onus is on the person who insists that his proposition is correct to prove it – the onus is not on an objector to prove that an unproven argument is incorrect (although for a number of reasons, too lengthy to state here, I believe that such a proof is not possible).
I think that you’re a bit confused in here, but in a way that might have a kernel of reasonability under it.
When you’re talking about languages, I think what you actually mean is more than just syntactic notation – it’s the semantics of the system that you’re working in. And it’s absolutely true that Cantor’s proof is specific to the semantic system of axiomatic set theory. It’s built from the set theoretic concept of cardinality and the set theoretic notion of cardinality comparison.
You can build a valid axiomatic system in which it’s not true. You can build different mathematical systems with different properties. It’s possible and even reasonable to build a mathematical system which _doesn’t_ include non-computable numbers. In a system like that, the set of “real” numbers (the computable reals) has the same cardinality as the set of integers. But it’s not the same system of mathematics that we’re talking about.
Mathematics is a set of systems, and the base of all of those systems in the way that we talk about them most of the time is axiomatic set theory. When you talk about real numbers, what you’re talking about is a set of values defined as the equalence classes of the limits of Cauchy sequences over sets of rationals; and rationals are ratios defined by equivalence classes of ordered pairs over the set of natural numbers, and so on. If you want to talk about comparing the cardinality of the set of real numbers to the cardinality of some other set, then you’re stuck with the framework of set theory – because that’s the “language” in which they’re defined, the language in which their meaning is expressed.
Trying to talk about how the conclusions of applying set theory to the real numbers is wrong is like trying to talk about how the hebrew word “adamah” can’t mean earth, because in english, adamant is spelled with an A, and an uppercase A is pointy, but the earth is round. You’re mixing concepts that don’t make any sense.
The definition of A being a “bigger” set than B, with regard to cardinality, is nothing more than the fact that the image of every injective function from B to A is a proper subset of A, i.e. no injection is a bijection. An “enumeration” of a set A is precisely an bijection from the natural numbers to A. The proof that no proposed injection can be a bijection suffices to establish that the set of real numbers has cardinality larger than the set of real numbers. More generally, the same is done when comparing any set to its power set, giving us an unbounded set of infinite cardinals.
I was agreeing with Mark, by the way.
http://us.metamath.org/mpegif/ruc.html is a completely formal, computer-verified proof that the set of real numbers is larger than the set of integers.
An objector generally has a responsibility for bringing up problems with an argument. An original argument may put far more responsibility on the maker. But in any field, when a newcomer swoops in and makes an argument against a well-established fact, they’re probably wrong, and people trained in that field can’t afford to spend the time dealing with every such argument. An objector in that case needs to be clear and well familiar with the tools of that field to produce a clear and orthodox argument against that fact if they wish to sway people in the field.
First, can we please agree to not accuse each other of being confused? That’s unproductive.
As I have said before, I completely accept that the diagonal proof, when stated correctly in a given language system, proves that there can be no enumeration of real numbers in that language system. And that there are formal proofs that prove that there can be no function within that formal system that enumerates the real numbers of that language system. But I do not accept that that proves that there are “more” reals than natural numbers.
You belittle people who don’t use language that you consider sufficiently formal. But I don’t see that you have provided even a semi-formal proof that there can be “more” elements of infinite set than another. It seems to me that what you do is to appropriate common English words and attach a meaning to them that is completely alien to their common usage.
The typical argument that is given (such as that of Christopher McClain above) that there can be “more” elements of one infinite set than another goes like this:
Since the proposition that:
(there is an injection but no bijection from B to A)
is equivalent to:
(cardinality of A > cardinality of B)
is also equivalent to:
(the number of elements of A > the number of elements of B)
or in common English parlance A has more elements than B.
But the last equivalence only applies if the sets A and B are finite, and where the variable “number” has the domain of natural numbers. The assertion that we can extend the equivalence of cardinality and “more” to apply for infinite sets amounts to pleading that:
Since the number of elements of an infinite set is limitless, then if A and B are infinite, this becomes:
(there is an injection but no bijection from B to A)
is equivalent to:
(cardinality of A > cardinality of B)
is equivalent to:
(the number of limitlessly many elements of A > the number of limitlessly many elements of B)
But of course, that would be absurd, since there is no natural number that defines “limitlessly many”, it is not a member of the domain of “natural number”.
In short, pleading that different cardinalities of infinite sets “proves” that there are “more” elements in one set than another is an absurdity, where rather than actually providing a proof, a word in the English language is appropriated and everyone is told that they must accept an additional meaning (greater cardinality of an infinite set) besides the conventional English meaning.
If I may quote from your comment: “You’re mixing concepts that don’t make any sense.” Exactly!
Of course, if instead you can come up an actual proof there can be “more” elements of one infinite set than another then do please provide it.
I have two “by the ways” below, which are incidental to the main point.
1) You state that: “…Cantor’s proof…[is] built from the set theoretic concept of cardinality and the set theoretic notion of cardinality comparison.” It was only in 1874 when Cantor first provided a proof – that there is no enumeration of the reals – that the subject of cardinality of infinite sets was first envisaged. So it was that finding that precipitated the notion of applying the notion of cardinality to infinite sets, not the other way around.
2) I don’t agree that set theory is “the” language in which real numbers are defined. It’s “a” language in which real numbers might be defined. It would be nonsense if anyone suggested that there aren’t alternative ways of defining real numbers. Mathematicians were defining real numbers in different ways long before set theory was invented. Besides, when does one ever see a real number defined in purely set-theoretic symbols such those for “is an element of” “is a subset of”, etc? For sure, scientists and engineers don’t use such definitions of real numbers.
But all you’re doing is saying that you don’t like the definition of cardinality. Set theory does define a notion of cardinality. It’s quite well-defined, if you take the time to study set theory.
You’re basically arguing that we shouldn’t be allowed to say that the cardinality of the set of real numbers is larger than the cardinality of the set of natural numbers, because you don’t like the definition of cardinality.
You say things like: “But the last equivalence only applies if the sets A and B are finite, and where the variable “number” has the domain of natural numbers. The assertion that we can extend the equivalence of cardinality and “more” to apply for infinite sets amounts to pleading that…”
That’s simply not true. The set theoretic definition of equality *doesn’t* only apply to finite sets. It’s defined for *all* sets. You may not like that – but if you’re talking about set theoretic mathematics? What you like doesn’t matter.
The definition of cardinality isn’t limited to finite sets. Pick up any textbook on set theory: cardinality is defined in terms of 1:1 mappings; and using the axiom of infinity and induction, it’s applicable to any set, not just finite ones.
You don’t like that, because you don’t think that talking about “cardinality” makes intuitive sense for non-finite sets. But that doesn’t matter: it’s well-defined by the axioms of set theory. Your comfort doesn’t matter. Your dislike for applying tho concept of cardinality comparison to infinite sets doesn’t matter. You’re talking about mathematics defined under axiomatic set theory, and that means that you’re stuck working in terms of the definitions of axiomatic set theory.
You said “But all you’re doing is saying that you don’t like the definition of cardinality. … You’re basically arguing that we shouldn’t be allowed to say that the cardinality of the set of real numbers is larger than the cardinality of the set of natural numbers, because you don’t like the definition of cardinality.”
FACT:
I didn’t state anywhere that there one should not be able to state that one infinite set has a larger cardinality than another. I don’t have any problem with that, it merely indicates the direction of an injection. Please do not attribute arguments to me that I did not make. It’s unprofessional, bedsides the obvious straw man fallacy.
You also said “That’s simply not true. The set theoretic definition of equality *doesn’t* only apply to finite sets. It’s defined for *all* sets. You may not like that – but if you’re talking about set theoretic mathematics? What you like doesn’t matter.”
FACT:
I did not argue that equality only applies to finite sets. Perhaps you should read what I wrote more carefully before you respond. Hint: see “the last equivalence only applies if …”
Since it appears that my previous post was misunderstood, I will try to make it completely clear that I do not have any problem with the definitions of cardinality. So:
1) I accept that for all sets A and B (finite or infinite) the proposition that:
(there is an injection but no bijection from B to A)
is equivalent to the proposition:
(cardinality of A > cardinality of B)
2) I also accept that for finite sets A and B the proposition that:
(cardinality of A > cardinality of B)
is equivalent to the proposition:
(the number of elements of A > the number of elements of B)
or in common English parlance A has more elements than B.
but I do not accept it for the case where sets A and B are both infinite.
So let me say it again. I have no objection to the definitions of cardinality as being equivalent to the notions of injection of sets as indicated above.
And let me say my response again.
When you’re working in the world of set theory, you don’t get to pick and choose which definitions you “accept”. Axiomatic set theory defines a collection of rules for how you do reasoning. The set of real numbers (see that pesky word, “set”?) is defined by the rules of set theory to have certain properties. The cardinality of a set is defined in a particular way, by the rules of set theory, and that definition applies to all sets, not just the ones that you want it to apply to.
You can quibble about whether or not we can take the formal notions of set theory, and translate them into informal english words. But in my opinion, that’s just silly. If your entire point is “I don’t like it that people use the word “larger” to mean “has greater cardinality”, then I’d say go talk to some linguists. They’re interested in that kind of distinction. But people doing math don’t. When we’re talking about mathematics, everyone understands that english words are shorthands for mathematical definitions. When we say “size” of a set, we mean cardinality. When we say the size of one set is larger than the size of another set, we mean that it has greater cardinality.
Your number 2 makes no sense because in mathematics “number of elements” is identical to “cardinality”. There is no notion of “number of elements” other than “cardinality”. They are completely interchangeable. More precisely, “cardinality” is a well-defined mathematical term and “number of elements” is an English phrase which can be used to refer to “cardinality” when we are willing to relax formality.
So, as an analogy, we are operating in a world in which a=2 and b=3, and you are saying something like
“I believe you when you say that 2 < 3, but I refuse to believe that a < b"
which is nonsense.
Sorry for being a bit scattered; I’m traveling for work this week (in Stockholm), and I’m terribly jetlagged.
So: sorry, but when you talk about real numbers, you *are* talking in terms of set theory. The whole discussion is about the size of the set of real numbers. Take away set theory, and you discard the whole basis of the proof. Yes, you can create alternative definitions of the real numbers, but if you do, they’re not the same thing – they’re not the same set of real numbers.
As for scientists and engineers? They don’t actually use real numbers. Scientists and engineers work in terms of measurements. When I was a kid, my dad worked on the Galileo probe, and for trajectory computations for galileo, they used pi=3.1416 – none of the other measurements that were used were more precise than that, so using a more precise value for pi was useless. They were able to navigate a probe from earth to Jupiter using numbers no more precise than 5 significant digits!
In practice, we only use rational numbers. I’ve been known to argue that we’d be better off using a system based on the set of computable numbers instead of the set of reals: the reals have all sorts of objectionable qualities. (I find the obsession of people with Cantor funny, because the cardinality of infinite sets is a simple notion; there’s so much more weirdness that’s I find much harder to accept than just cardinality. Most numbers can’t be identified – they can’t be written, they can’t be computed, they can’t be described, they can’t be identified in any way. That’s a problem: as an intuitionist would happily point out, how can something exist if you can’t ever describe it? Cardinality is easy: I can show you how to compute the exception, even if the computation is infinite; but undescribable numbers? There’s a strong case to be made that they’re a nonsensical artifact of set theory. And yet… if we get rid of them, if we reconstruct the fundamentals of set theory to eliminate that artifact, we lose many other things that we really, really want.)
Continuing with the scientist and engineer theme: most scientists and engineers don’t care about number theory. The engineer who designs the engine in your car doesn’t know diddly-squat about what’s happening on a quantum level to the molecules of fuel burning inside of the cylinder of the engine they’re designing. They know how the gases act as a gas, how they burn, what products the burn produces, how energy can be extracted by it, etc. They don’t understand the deep fundamental level, because there’s just not enough time to be a master in both quantum mechanics and engineering. Similarly, as a software engineer, I have very little understanding of how electrons moving around the chips in my laptop turn into computation. That doesn’t mean that it’s not happening.
I would clarify that scientists and engineers use both transcendental and irrational algebraic numbers to the extent that they refer to them in theoretical formulas, and a case can be made that even in practical measurement there may be some inclusion of irrational constructible numbers like the square root of 2, but you are absolutely correct that when they finally get around to actual computations that are actually directly used, their world is discrete, as dictated by their binary partners in crime.
It’s not even limited by computers: my dad taught me about precision long before I saw my first computer. Scientific work is limited by measurement, and all measurements have limited precision. There are a range of tools that engineers and scientists use for managing precision, like error bars or significant digits, and they’re important whether you use a computer or not.
Yes, I agree.
You say: “sorry, but when you talk about real numbers, you *are* talking in terms of set theory.”
That’s opinion, not fact.
It might be fact that when you talk about real numbers, you are talking in terms of set theory. But it is your opinion that when I talk about real numbers, I am are talking in terms of your set theory.
You say “you can create alternative definitions of the real numbers, but if you do, they’re not the same thing – they’re not the same set of real numbers.”
Clearly, it’s your opinion that in the entirety of your definitions of set theory, the resultant set of real numbers is a superior set to any set of real numbers given by any other possible definition. You cannot imagine that 300 years from now, there might actually be a better theory of numbers than what conventional ZF set theory provides. That is breathtaking arrogance.
That reminds me of the following quote:
‘My theory stands as firm as a rock; every arrow directed against it will return quickly to its archer. How do I know this? Because I have studied it from all sides for many years; because I have examined all objections which have ever been made against the infinite numbers; and above all because I have followed its roots, so to speak, to the first infallible cause of all created things’
Cantor wrote this in 1888. Thirteen years later, Russell’s paradox demonstrated that Cantor’s theory of sets as it was then was contradictory, and had to be patched up by axioms such as ZF.
No, that’s *not* opinion: that’s mathematics.
We’re talking about the set of real numbers, and a proof concerning the cardinality of the set of real numbers.
You don’t get to decide that you accept some conclusions of axiomatic set theory and the theory of real numbers built on it, but reject others on an ad-hoc basis.
That’s the entire point of my original post. We’re talking about formal concepts, not informal ones. There’s a reason why we use formalisms.
You can construct sets of numbers in many different ways. You can certainly create an alternative definition of numbers. For example, Knuth and Conway put together a really interesting construct called surreal numbers. In that construction, you can define sets and cardinality in different ways than the way that we talk about it.
But that’s not what we’re talking about here. Here, we’re specifically talking about Cantor’s framework of sets and cardinality. We’re talking about the set of real numbers, as defined by the set theoretic foundations and the set theoretic theory of real numbers. There’s no opinion here: we’re talking about a proof that’s only meaningful in a specific semantic, logical, and mathematical framework.
If you take the conclusions of that framework, and drop them into an entirely different semantic framework, then you’re wrong. When we talk about comparison of set cardinality, we’re doing it in the realm of sets and cardinal numbers.
You don’t get to argue that the frequency of a beam of red light is larger than the frequency of a beam of ultraviolet light, and then say that it’s just an opinion that you’re wrong, because you think that we should be comparing wavelength instead of frequency, and the wavelength of red light is longer than the wavelength of ultraviolet. That’s not an opinion: that’s just taking a comparison that’s meaningful because of a specific definition of what you’re measuring, and rejecting that definition but still trying to discuss conclusions that are only meaningful in the context of the definition. That’s what you’re doing: taking a word that’s got a very specific, formal meaning, and then insisting that it’s just opinion that that’s it’s meaning.
If you reject the way that cardinality comparison is defined, that’s very nice for you. But it’s got absolutely no bearing on the conclusion of Cantor’s proof, because Cantor’s proof is talking specifically about what the word “larger” means in the context of cardinality.
To put it a slightly different way: if I go to a paint store, and I ask for paint that’s a specific shade of blue in the Pantone spectrum, I don’t get to return the paint for being the wrong color because the Pantone spectrum definition of that shade of blue is wrong. I asked for the paint *in that system*, and so the definition from that system is right in that discussion.
To expand one important point, that I think I glossed over a bit in the previous comment:
If, a hundred years from now, people are working with a different foundation for mathematics, it’s possible that Cantor’s reasoning about cardinality will no longer make sense. It could change for technical reasons, if someone finds a better foundation; it could change for stylistic reasons. But if it changes, then *in that new framework*, you could have different results.
And yet, that won’t affect anything about Cantor’s proof. It will still be the case that in the formal system in which it’s defined, Cantor’s proof is valid, and the cardinality of the set of real numbers is larger than the cardinality of the set of natural numbers.
Mathematical facts aren’t absolute facts: they’re facts within a formal system of reasoning. The only thing that will change the fact that in set theory, the cardinality of the real numbers is larger than the cardinality of the naturals is someone proving that axiomatic set theory is inconsistent.
(And we’ve got some pretty solid proofs that it is consistent up to the limits of the formal reasoning itself.)
Mark’s point here is better than mine below. If we wanted to be verbose in the statement of Cantor’s result, we could explicitly preface it with “Using the following specific definitions of “set”, “cardinality”, “real numbers”, … then the following result holds.”
Your last sentence makes our point and undermines your own: ZF axioms (or other sets of axioms) are necessary to make sets well-defined.
The terms “set”, “cardinality”, and “real numbers” as Mark has been using them are well-defined. Your suggested alternatives of “number of elements” and “other ways to define real numbers” are not well-defined, at least not yet by you.
Modern mathematics requires well-defined terms. In order for mathematics to be on firm ground, we have had to clear up the notions of “convergence”, “continuity”, etc which has impacted our definition of “real numbers”.
The only well-defined notion of “number of elements” presented thus far is “cardinality”. If you would like to suggest that there is a definition of “number of elements” that is distinct from “cardinality” for infinite sets, then you must provide a precise definition to be taken seriously within mathematics.
It is no longer acceptable to loosely use phrases that “capture the idea” of something in place of a precise definition. The phrase “something with direction and magnitude” may capture the idea of a vector, but technically a vector is an element of a “vector space” which has a precise definition as a set with specfic properties. Likewise “points on a line” or “signed lengths” may capture the idea of a real number, but are not acceptable definitions. Acceptable definitions include lists of properties, including least upper bounds or dedekind cuts or cauchy sequences. The whole history of real numbers includes increased realization that we didn’t have good enough definitions to precisely indicate what the heck we meant, and now the axiomatic definitions are the de facto definitions that are acceptable.
Again, to echo and perhaps summarize Mark’s comments, when talking about the set of real numbers, there is no distinction between “cardinality” and “number of elements”, and there is no distinction between “A is larger than B” and “there exists an injection but no bijection from B to A”. In mathematics that is based in set theory, there are no other well-defined notions of “number of elements” and “bigger”. And there is not some a priori notion of “real numbers” about which we may be having a merely semantic disagreement. The name “real numbers” refers precisely to a set defined in one of several ways within axiomatic set theoretic mathematics. It is a specifically defined abstraction, not a vague reference to numbers or measurements we encounter in real life.
In natural English, if you take a group of things and add more things, the second group has more things than the first. One might argue about the natural English idea that the set of the natural numbers is the same size as the set of the prime numbers, but I don’t see how you can argue that the set of the real numbers aren’t larger than the set of the integers from a natural English perspective.
You see a real number defined in purely set-theoretic terms in Intro to Modern Analysis. Like always, once you get to higher level concepts, you don’t get it in raw set theoretic terms, but everything is ultimately defined by set theory.
I’d accept that real numbers don’t have to be defined in set theory. But the size of the set of real numbers has to be. You could choose a different theory to discuss the size of sets, but as far as I know there’s no general purpose theory that includes what’s thought of as real numbers that would give you a different answer.
Yes, I agree.
Mark, You try to have it both ways.
On the one hand you claim that the diagonal proof must be stated within a valid formal framework. But on the other hand your claims are based on arguments outside of that framework.
Within such a formal system as you refer to, every statement in that system and the objects of that system have to be in the language of that formal system. And that means that in your diagonal proof in that system, every number, reference to a number, every enumeration function, every reference to an enumeration function, and every definition, including the definition of the diagonal number, must be in the language of that system.
And since you have at least some knowledge of Godel and incompleteness, you must know that you can also make statements outside of such a system regarding the statements of that system. But you refuse to allow anyone to consider the diagonal proof except as within your formal system.
Now, in such a formal system, you can of course obtain the result that there can be no enumeration of all real numbers within that system. But that does not prove the case where the enumeration is in a meta-language to the system. Either you can provide a proof that a diagonal number can be defined where the enumeration is in a meta-language to your formal system, or you cannot. I did reference this before and you said I was confused, and you didn’t address the content. But I’m not confused, and I haven’t forgotten. I already asked you for such a proof, but that was not forthcoming. And I suppose you won’t attempt to provide such a proof, since you insist on insisting that you will only consider working within your formal system.
Since that is the case, what you are able to prove is that there can be no enumeration of the reals within your formal system. That’s all.
Given only your in-system diagonal proof, you have no basis for asserting that there “exist” real numbers that have no finite definition. Attempts at such a proof (as in Konig 1905 Über die Grundlagen der Mengenlehre und das Kontinuumproblem) require the introduction of a meta-language. So, given your self-imposed restrictions, you can’t even attempt to prove that your notion of “more” applies in that sense.
But, of course, it is abundantly obvious that you are nevertheless claiming that you do have a proof that there “exist” real numbers that have no finite definition (both in this post and throughout your site) – and by so doing, you are stepping outside of the formal set theoretical framework that you espouse in such depth here.
As I said, you try to have it both ways.
I’m not falling for that deception, and neither should anyone else.
A proof is not about language, it is about understanding. If you have a perfect proof that you don’t understand, what good is it. It would simply allow you to believe something that you don’t understand, this is called faith based mathematics.
If you can’t explain a proof to a fifth grader, then you probably don’t understand the proof yourself.
Consider this “proof” that concludes the cardinality of the irrationals are less than or equal to a set of rationals. Is it formal? Is it valid? Is it understandable? Where does it go wrong? Just peek at the link below and see.
http://quicklatex.com/cache3/a4/ql_b4ad1371f109078925c72d20e49231a4_l3.png
Actually, no.
The point of formal mathematics is that a proof is a purely mechanical exercise. In practice, we rarely achieve that level of perfect formality, but that’s the goal.
The real point of logic is to mechanize proof. Given a set of axioms, and an interesting statement written symbolically, you should be able to perform the proof without any clue of what any of the axioms mean, or what any of the symbols in the statement to be proved mean. Logical proof is deliberately mechanistic, literally. The origin of the field that we call computer science started, largely, with mathematicians trying to build fully mechanistic proof systems.
If a proof “depends on understanding”, what that really means is that it depends on some unstated assumptions. The hardest part of proofs comes from that: we find it very difficult to lay out every single assumption, and every logical inference that forms a proof.
Mark, you are not making this easy for me. It has been said…
“The less he understands something, the more firmly he believes in it.”
Cantor wanted to know if there were more real numbers than natural numbers. So, he listed the natural numbers and paired them with the purported list of all real numbers and found that the list of real numbers was incomplete, and he incorrectly concluded that the real numbers have a greater cardinality.
He could have paired the purported list of real numbers, with a subset of the natural numbers, like this…
14 r1
144 r2
1444 r3
14444 r4
etc…
Then every real number on his list is paired with a natural number and if he finds real numbers that are not in the list, he still has plenty of natural numbers that he can pair with the new found numbers.
24 rr1
244 rr2
2444 rr3
24444 rr4
etc…
And we could do this forever, so can you “understand” why his diagonal proof is a proof of nothing?
All the formality in mathematics will not tell you about Cantor’s hidden assumption, that you must list the natural numbers in order and in one list, when there is no reason why that must be so.
Also, there was a typo in the proof that I posted in my previous post, which is fixed in this link…
http://quicklatex.com/cache3/ed/ql_9efce1124e284917e511a1c4d548fced_l3.png
Cantor’s proof *doesn’t* require any particular ordering to his list of natural numbers. All it requires is that the list of natural numbers be complete. If you don’t understand that, then there’s simply no point in talking anymore.
Set theory defines the way of comparing the size of two sets. What it says is: if there exists a one-to-one mapping – any one to one mapping – between two sets, then those two sets have the same cardinality. If every way of producing a one-to-one mapping between two sets leaves elements of one set unmapped, then that set has a larger cardinality.
What Cantor’s proof concerning the cardinality of the real numbers does is show that given any possible mapping from the natural numbers to the reals, there will be real numbers that are omitted. It doesn’t rely on any particular mapping, or any particular ordering of the natural numbers. Since they’re the natural numbers, it’s most convenient to write them down in the standard order. But you can reorder them in any way you want: the order doesn’t matter. No matter what games you play, the Cantor diagonalization shows that given any purported one-to-one mapping between the integers and the reals, it will be incomplete in the reals.
The purported counterexample that you’re showing doesn’t actual do anything. It fails immediately, because it’s building a mapping between a set of natural numbers and the reals, but not the set of all natural numbers and all reals. All that you can prove with that example is that the set of real numbers is larger than the subset of the naturals that you’re playing with – and Cantor’s proof does that quite nicely: it generates a real number that isn’t covered by your mapping.
Mark said, “If you don’t understand that, then there’s simply no point in talking anymore.”
Just the opposite is true, as long as I disagree with someone, there is a point in talking. There is not much point in talking about things that you agree with, i.e. echo-chamber.
Mark said, “Cantor’s proof *doesn’t* require any particular ordering to his list of natural numbers. All it requires is that the list of natural numbers be complete.”
Where did you get this idea about complete? It is wrong.
There is a simple problem that very few people can solve because they can’t think about drawing the lines “outside the box”. Can you connect these 9 dots with four straight lines?
. . .
. . .
. . .
The reason why you are not understanding Cantor is because you are not “thinking outside the box”.
What you say is true, it is possible to show that two sets are equivalent if you can find a bijection between them. This would be a sufficient condition, but it is not a necessary condition.
We can also show that two sets are equivalent by showing that there exists an injection from one to the other and vice versa. If f(N) -> R and g(R) -> N are both injective functions then |N| = |R|. This is known as the Schröder–Bernstein theorem.
An injection from the naturals to reals is trivial.
1 -> 0.1
2 -> 0.2
3 -> 0.3
->.314159…
4 -> 0.4
…
10 -> 0.01
->0.271828…
11 -> 0.11
->0.141421…
12 -> 0.21
…
Every natural number will be paired with one and only one real number. Since there are real numbers in the codomain that don’t have a partner, this is not a bijection but it is an injection.
Then to show that the sets are equivalent we need only find an injection from the reals to the naturals.
Here is an injection from a list of real numbers to a list of natural numbers.
0.5123453… -> 4
0.5125674… -> 44
0.5124195… -> 444
0.5123676… -> 4444
0.5127295… -> 44444
…
It is not enough for you to say is that there are real numbers in the set of real numbers that are not in the list, because I can say the same thing, there are natural numbers in the set of natural numbers that are not in the list.
It is up to you to prove that you can produce more real numbers than I can produce natural numbers.
If you can’t produce the proof, then your claim that there are more real numbers than natural numbers fails.
No, there’s no point continuing a discussion when it’s reached the point of “is not, is too, is not, is too”.
You’re continuing to play the same silly games, and I’m continuing to respond with the same old boring refutations. (And the old “thinking outside of the box” thing has gotten so old and cliched that even bringing it up is, basically, thinking inside the box.)
You’re continuing to talk about concepts that are well defined in set theory, and trying to pretend that they aren’t, or trying to pretend that you can shoehorn other things into them. You keep finding silly new ways of doing it, but it’s always the same game.
You’re mangling Shroder-Bernstein quite badly here. S-B doesn’t say “If there’s an injection from A->B, and an injection from B->A, then |A| = |B|”. In fact, it’s a whole lot more complicated than that. I’m not going to teach you an advanced course in set theory here – but S-B creates a set of requirements on the two injections which mean, essentially, that if one of the two sets is the set of natural numbers, then the two injections together define an enumeration.
(When it involves the natural numbers, S-B isn’t a particularly interesting theorem – because what it says is: an infinite set has the same size as the natural numbers if you can define an enumeration of the set. It becomes interesting when you try to apply it to non-enumerable sets. Like, for example, topological spaces, the set of real numbers, etc.)
And so, we continue to spin our wheels. You continue to try to handwave your way around the fact that within the mathematics of set theory, none of your objects make any sense at all. And I keep explaining that if you want to refute a proof in the system of set theory, you need to work inside of the system of set theory.
It’s becoming a bit of a gish gallop. It’s meta-systems. No it’s Shroder-Bernstein. No, it’s Godel. No it’s an enumeration which isn’t an enumeration. No, it’s a different language. No, it’s this, it’s that, it’s the other. But never do you actually bother to present an actual mathematical argument, or address any of the problems that I’ve repeatedly pointed out. Just this unending stream of nonsense.
While Mark’s reply is on point, I have a more succinct one for you, Carl:
Define “list”.
“If you can’t explain a proof to a fifth grader, then you probably don’t understand the proof yourself.”
If you can’t build an space shuttle with household items, then you probably don’t know how to build one.
You see, Mark, in principle you and I seek the same thing.
Everything proven logically and without intuition and without unstated assumptions.
Mark, again you are trying to have it both ways.
As I have noted already, on the one hand you assert that you will only consider the diagonal proof in terms of within ZF set theory, but on the other hand, you assert a result that is not derived from a proof within ZF theory, or for that matter, from within any given formal system.
It seems to me that you only respond to comments that you find easy to answer; the more difficult ones you ignore and hope that no-one notices. I notice.
In your post of January 24, 2018 at 9:04, after I pointed out the above, you asserted that:
“Cantor’s proof …[shows] that given any possible mapping from the natural numbers to the reals, there will be real numbers that are omitted.”
Well, no, as I have already pointed out, if you are committed to a formal proof within a formal system, then you cannot prove anything regarding an enumeration of the reals that is defined outside that system, i.e., in a meta-language to that system, such as by a dictionary style listing of the symbol sequences of that system, without any regard to their meaning.
You just keep playing with weasel-words to evade things. There’s nothing particularly complicated here.
It doesn’t matter how you define a supposed enumeration of the reals. All that matters is that it *is* an enumeration of the reals, and set theory defines what that means.
If you’ve got something defined completely outside the bounds of ZF set theory and the real number theory that’s defined using that, you’re not talking about Cantor’s proof anymore. Cantor’s proof is a proof in the axioms of set theory and real number theory.
You can play games all you want with systems that aren’t part of the world of set theory. As I’ve said numerous times, it can be an interesting and valuable thing to do. But when you do, you’re no longer doing set theory. Cantor’s proof applies within the realm of set theory. It’s very precisely defined in terms of the objects and entities that exist in that mathematical realm. It doesn’t pretend to apply to anything outside of that space. And that’s fine, because we all understand what that means.
You can use nonsense terms like “meta-language to the system”, which is exactly the kind of informal term that I disdain. In terms of math, saying “meta-language” doesn’t mean anything unless you define it. But in terms of Cantor’s proof? It doesn’t matter.
Cantor’s proof is a very simple construction. There are two key pieces to it.
The first says that we’ve got a representation of every possible real number in terms of infinite sequences of digits. No matter how you generate them, every real number can be represented in terms of an infinite sequence of digits. Give me a real number, and I can find its representation.
The second says, ok, you claim to have an enumeration of all of the real numbers. I’ll show you how to produce a real number that isn’t part of that enumeration.
You can talk about undefined meta-systems all you want, but those two steps are still a fundamental barrier. Every real number can be represented as an infinite sequence of digits. And for every supposed enumeration of real numbers, I can produce a real number that isn’t in that enumeration.
The only way around that is by playing a nonsense game with words: you can redefine “real number”, or you can redefine “enumeration”. But neither of those refutes Cantor. You can babble about “metasystems”, but when you get to the point of Cantor’s proof, either you have an enumeration, or you don’t. Either the values in it are real numbers, or they aren’t. Cantor’s proof doesn’t care how you generate the enumeration.
Mark, this is not regarding the primary content of your last post, but there are things that have to be said regarding your misconceptions re meta-language. You said: “You can use nonsense terms like ‘meta-language to the system’, which is exactly the kind of informal term that I disdain. In terms of math, saying ‘meta-language’ doesn’t mean anything unless you define it.”
Mark, the notion of metamathematics/metalanguage has been well known and used in mathematics for at least 85 years. Gödel used metamathematics in his incompleteness proof (in fact you eulogise that proof, and you have said: “I’m absolutely fascinated by Kurt Gödel, and his incompleteness theorem. Incompleteness is, without a doubt, one of the most important, most profound, most surprising, and most world-changing discoveries in the history of mathematics.”).
So I’m afraid that both the facts and other things you have said contradict your assertion “saying ‘meta-language’ doesn’t mean anything unless you define it”. It might not mean much to you but that only indicates that you have not given that aspect of mathematics sufficient study. And your statement that “You can play games all you want with systems that aren’t part of the world of set theory” throws out a huge part of mathematics. In fact, if you want to talk about mathematics, rather than actually doing it, then you are doing metamathematics. In fact, nearly all of your blog site is metamathematics. That’s a fact. If you want to scrap all the metamathematics from your site and leave only pure formal set theoretical statements that’s fine by me. But if you don’t do that, then to tell others that they can’t talk about mathematics in the same metamathematical way that you do is sheer hypocrisy.
By the way, you previously said: “the real numbers means something very specific: it’s the unique complete totally ordered field …”
Sorry, Mark, that’s not set theory, the definition of such fields is in a meta-language to set theory. It would be a classic blunder of logical inference to suppose that because certain sets of ZF theory satisfy the definition of a complete ordered field, then that must mean that everything that satisfies the definition of a complete ordered field is a ZF set. There can be many different kinds of formal systems whose entities satisfy the field definition.
You have the gall to speak disparagingly of “playing a nonsense game with words and babbling about ‘metasystems’ “, yet you hop in and out of set theory to define real numbers, while at the same time insisting that you are only prepared to consider what can be said within set theory.
If you had apportioned more study to metalanguage and metamathematics, instead of rubbishing them, perhaps you would not have made such an elementary error.
I’m not objecting to the concept of metalanguage: I’m objecting to the way that you’re using it.
Like so many other things in math, there’s a way of precisely defining metasystems. That doesn’t mean that every use of the word “metasystem” is meaningful. For one prominent example, Chris Langan likes to talk about metasystems in his CTMU, but he never bothers to define what a metasystem is.
The reason that I keep saying you’re playing a nonsense game is because you keep insisting on things that you don’t define.
You keep trying to play a game where, by using imprecise language, you try to weasel concepts from outside the realm of set theory and the theory of real numbers defined using set theory without defining them in the language of set theory.
And that’s a big deal. A mathematical theory require mathematical definitions. To use a concept in a proof, that concept needs to be defined in the same system as the proof.
The brilliance of what Gödel did is that he took the entire system of set theory and first-order predicate logic, and figured out how to express it within the framework of axiomatic set theory and Peano arithmetic. He didn’t rely on anything that didn’t work in AST&PA. His proof is completely honest and clear about the fact that what he’s doing relies on that framework. He didn’t create some undefined “metasystem” and then insist that it was allowed to do things that couldn’t be specified in ZFC&PA. Gödel’s metasystem doesn’t change anything about the basic mathematical framework it exists in. In fact, it’s entire point is that it shows that you can take any logical system that’s valid and consistent under ZFT+PA, and express it entirely in terms of primitive recursive (as defined in ZFC+PA) arithmetic computations (as defined in ZFC+PA).
The problem with your metasystem talk is:
(1) you never define what you mean by a “metasystem”. It could be anything from an arithmetic construction like Gödel, or a bunch of hand-wavy nonsense. Since you never bother to define it, the reasonable assumption is that it’s the latter.
(2) you argue that because some unspecified metasystem that goes beyond ZFC + real numbers can produce something that violates Cantor’s proof, Cantor’s proof must be wrong. That’s not how mathematics works. Under any mathematical system, there will always be constructs from different mathematical systems that don’t make sense. I can write proofs about the surreal numbers, which are a strict superset of the reals, but those proofs may not be valid when spliced into real number theory, because they rely on concepts and constructs that don’t exist in RNT.
(3) Cantor’s proof doesn’t depend on how an enumeration of the reals is generated. It can be any magical metasystem you want: at the end of the day, if it’s a refutation to Cantor’s proof, then it needs to produce an enumeration of real numbers, and that enumeration needs to be the thing that set theory means by the term “enumeration”. If it produces an enumeration as defined in axiomatic set theory, then Cantor’s proof applies, and shows how to construct a counterexample. If it’s not an enumeration as defined in axiomatic set theory, then it’s meaningless to talk about it with respect to Cantor’s proof, because Cantor’s proof is specific to the set theoretic notion of an enumeration.
You want to have it both ways: you want to say that you’re refuting Cantor’s proof, but at the same time, you want to have the ability to play with concepts and constructs that have nothing to do with what Cantor’s proof talks about. And you want to say that that’s a justifiable thing to do, because you have a “metasystem” that you never bother to define.
Honestly, at this point, I’ve had enough of this – we’re just going in circles. If you’re right, you’re wasting your time arguing with a petty nobody of a computer scientist; just write a paper, and go get it published, and take home your Field’s medal.
Regarding the main subject matter of your last post (January 24, 2018 at 7:50 pm)
You state: “…every real number can be represented in terms of an infinite sequence of digits. Give me a real number, and I can find its representation.” And later, “Every real number can be represented as an infinite sequence of digits.”
That’s a common fallacy. But I’ll make it easy for you to try to prove me wrong. Just give me the representation of any irrational as an infinite sequence of digits. Do that and I’ll concede.
But of course you can’t. But what you can say is that given any valid definition of a real number, you can generate the digits of its expansion in any given base to as many digits as you want – but you can’t generate them all.
Note that in Cantor’s original diagonal paper of 1891, he writes the entities of an assumed enumeration as:
Suppose we have:
E1 = ( a1,1, a1,2, …, a1,ν, … ), E2 = ( a2,1, a2,2, …, a2,ν, … ), …
but of course that isn’t the way you will do it within your formal set theory.
No, in your formal proof, you refer to a real number as a particular type of set (because all entities within your set theory are sets). So any enumeration within set theory is an enumeration of sets, for example, as a set of ordered pairs of sets.
So, within your formal set theory, to refer to sets in general, you need variables whose domain is sets. Fine. No problem. So you go through your proof and you obtain a result something like this:
For all sets of ordered pairs {A, B}, where A is set that satisfies a certain definition (for natural numbers) and B is a set that satisfies a certain definition (such as real numbers), there does not exist a set of ordered pairs {A, B} such that the ordered pairs include every B. (Note that this is not prescriptive, it’s an informal description of the type of result you might get. Sorry, but that is the nature of metamathematics.)
So, within set theory, you can have a result that states there is no enumeration of sets of a certain type within that theory. In case you imagine that I have a problem with that – I don’t. It’s the additional informal nonsense that is assumed to follow from that which I object to.
I note that you say you hate that sort of informal nonsense too.
Now, given such a result of set theory, please tell me (and the rest of the world) how you obtain from that – WITHIN set theory – your assertion that there exist sets (that represent real numbers) but which have no finite representation.
You see, from a set theoretical result, the only information is that there are always some type B sets that, regardless of whatever enumeration, are missing from that enumeration. That doesn’t tell me that there exist sets that have no finite representation.
You often respond to comments by saying about something that it can’t be said/done within set theory. Well, I’m saying that now about your claim that there exist sets that have no finite representation.
You say that I am the one that is “playing with weasel-words to evade things”. But while you keep asserting that there exist sets that have no finite representation, you have yet to say how that might be proved within set theory. After all, this page is about “why we need formality in mathematics”. Exactly!
So please tell me, I’m dying to know, how you think that it can be proved within set theory that there exist sets that have no finite representation. No need for evasion or weasel words. Just a straightforward explanation will do.
Once again, what you’re doing is rejecting things that are fundamental parts of set theory.
By the argument that you’re making, Cantor’s proof fails far earlier: you’re arguing, in essence, that it’s impossible to specify the decimal expansion of an infinite real – so Cantor’ proof can’t ever produce a number, because it’s got a non-terminating, infinite representation.
But mathematically, that’s not a problem. The definition of how we represent numbers, the definition that we use to talk about the representation of a number – that doesn’t rely on termination. It relies on specification, using the axioms of infinity and induction.
So again: your problem isn’t with Cantor’s proof. You’re continuing to object the set-theoretic conclusion of a set theoretic proof, on the basis that you don’t like the underlying axioms of set theory.
Fine. As I keep saying: if you think that set theoretic math is wrong, you’re welcome to choose a different framework. You can build a different mathematical foundation, which doesn’t include anything like the axiom of infinity, or which has an axiom of induction which doesn’t allow induction over infinite sets. There are many different ways of doing that. But when you do that, you’re not refuting Cantor’s proof. Cantor’s proof is still correct within the framework of set theory.
Finally: how can I prove that there are sets without finite representation in set theory? Very easily: it’s a fundamental part of the basic axioms of set theory. In the ZFC construction, the axiom of infinity gives me an initial infinite set; the axiom of powerset gives me the ability to create a non-enumerable infinite set from the initial infinite set provided by the axiom of infinity; the axiom of specification allows me to define a wide range of infinite sets, both enumerable and non-enumerable. And from those, I can then directly move to defining the set of natural numbers; then using the set of natural numbers, I can construct the set of rational numbers; and then using the set of rational numbers, I can create the real numbers; and then using the set of real numbers, I can perform Cantor’s proof.
As I keep saying: you’re trying to take an intuition about infinity, transplant it into a proof based on set theory, and then demand that there’s a problem with that proof because it doesn’t match your intuition.
It’s fine to reject axiomatic set theory. There are great mathematicians who have done that. But you have to admit that that’s what you’re doing.
Mark, if you are going to totally misrepresent what I said, that’s up to you. But any intelligent person reading these comments will see through that misrepresentation. It seems to me that instead of actually addressing what I am saying, you are attacking a collective caricature of various people who have frequented your site – a straw man of your own creation.
But of course, it’s all an attempt at a diversion from the key point that you keep evading.
I said that if you want to confine everything to within set theory, that’s all right by me. And all I asked for – a simple request – is a sufficiently formal proof within that set theory that there exist real numbers that have no finite representation.
In response, all you did was provide one paragraph about how easy it would be “prove that there are sets without finite representation in set theory”, but what you actually did was talk about how easy it would be to prove that there is no enumeration of sets such as the real numbers in that set theory – but I’m not disputing that.
So, I ask again, please provide a proof within set theory that there exist real numbers that have no finite representation.
Before I get to anything else, let me point out again the Gish gallop that you’re pulling here.
Look at your last comment. The entire thing never mentions the supposed problem about real numbers with no finite representation. Instead, it goes off into a long nonsense discussion about how you don’t need to actually have a 1:1 mapping between two sets to show that they’ve got the same cardinality, based on a really silly mangling of the Shroder-Bernstein theorem. So when I respond to that, suddenly, you’re talking about something else entirely.
See, you’re continuing to play the same game. You refuse to define terms in a precise way, which gives you an easy out. You switch topics whenever you’re caught out on a mistake. And as you demand formality from me, you continue to refuse to define anything in a formal way. What do you mean by real numbers that have no finite representation? That’s one of those informal terms that sounds nice, but could mean several different things. Does it mean a number with no finite decimal expansion? Does it mean a number with no computable representation? Does it mean a number with no finite logical specification? Does it mean something else entirely? I can answer your supposed challenge in many ways – but no matter which one I choose, you’ve left yourself room to sneer, insult me some more, and say that I’m not answering your question.
For example, I can pull out one of my favorite family of infinite, transcendental, non-computable numbers: Chaitin’s Ωs. It takes quite a bit of mechanical reasoning, but an Ω is a number that for a particular recursive system (a formal mathematical abstraction of a computing device) encodes halting probabilities of programs under that computing system. Fully defining a recursive system is complicated and well beyond the scope of a comment on a blog (but if you care, there are numerous textbooks that work through the complete definition!) but it is a well-defined formal system built on the base of ZF set theory and first order predicate logic.
Given an effective computing system, we can model it as a function φ. φ operates on one parameter, which is a program that will be executed by φ. The size of the program
is the length of the program in bits.
Given this, we can define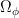
as:
That definition is valid under ZFC set theory, using the standard construction of recursive systems. It uniquely defines a specific number. That number cannot be computed – only approximations of it, and even those can be immensely problematical to actually compute. If we knew the value of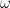
, we’d be able to construct a perfect (if ludicrously slow) halting oracle.
Of course, you can easily weasel out: you can say that I just wrote the definition of the number in a finite form right up there in that equation. Or you can say that that doesn’t really define the number because I can’t tell you its digits. Or you can say that it doesn’t count, because I’m bringing in recursive function theory, which isn’t set theory.
This is what I mean about this being a waste of time. You just keep flinging words, changing the subject, and playing definitional games. There’s no way that you’ll ever admit that you’re wrong.
But as I said before: if you really believe you’re right about this, it’s incredibly foolish to sit around and argue it on a blog. I’m not a mathematician. I’m just a lowly software engineer with a math fetish. If you’re right, if you can actually refute Cantor’s proof, then you’re a world-class mathematician who’s in a position to overturn the entire history of 20th and 21st century mathematics. If you genuinely believe this, you should be working to get your proof published, not wasting time arguing with some twit on a blog. If you really believe you’re right, you’re in a position to take home the field medal, take a faculty position in the university of your choice, and go down in history as one of the greatest mathematicians of all time. So what are you doing here?
Mark, you seem to be conflating my comments with those of a certain Carl, and ascribing things to me that should be ascribed to Carl.
Anyway, you ask me:
“What do you mean by real numbers that have no finite representation?”
You ask me now? After saying in a previous comment you said it was very easy to “prove that there are sets without finite representation in set theory”? And also you have described and explained it several times on your blog (do a Google advanced site search for the phrase “finite representation”).
And now you ask what it means? Is that intended as a joke?
For the umpteenth time, you have said you will only discuss the diagonal proof in terms of set theory. And for the umpteenth time I am asking you for a proof within that set theory that there exist real numbers which have no finite representation.
Just leave out the irrelevant stuff like Chaitin’s number, Fields medals, your pleas of, “I’m not a mathematician. I’m just a lowly software engineer” that contradict your claim that you know good math from bad math, and so on, and so on – and just provide that proof you said it was very easy to prove.
My apologies for confusing names. I’ll try to keep that straight.
As I said, the phrase “finite representation” is an informal term, which could be assigned to many different meanings. I gave you some examples of what it could mean, and yet, still, you refuse to bother to actually provide a definition. Why?
Which one?
(1) A number has an infinite representation if its decimal (or binary if you prefer) expansion has an infinite number of digits.
(2) A number has an infinite representation if its expansion in every integral number base has an infinite number of digits.
(3) A number has an infinite representation if its expansion in every integral number base has a non-terminating, non-repeating sequence of digits?
(4) A number has an infinite representation if there is no finite-length program in a recursive computing system that produces its digits.
(5) A number has an infinite representation there is no way of uniquely identifying the number in a finite amount of space.
You call Chaitin’s number nonsense. Why? It’s an example of a number which (under several possible definitions – 1, 2, 3, and 4 above!) has no finite representation, which therefore proves that there are real numbers in set theory with no finite representation. But you reject it, out of hand, sneering that it’s irrelevant, but without bothering to state *why* you’re rejecting it.
That’s the problem with not having a formal definition. There’s no way for me to actually do what you claim to be asking for. Like I keep saying: the game you’re playing is based on keeping everything fuzzy enough that you can’t be refuted. I’ve given you an example of a number with no finite representation – but you’ve rejected it without explanation. You’ve refused to define your terms no matter how many times I ask, and you reject examples of the things you’re asking for, on the basis that they clearly and obviously don’t meet the requirements of the definition you refuse to share.
So gosh, why would I say that you’re not arguing honestly?
It’s a common trick to pretend that you don’t know what someone means and to keep asking for definitions ad nauseum. We could both play that game, I could say that you referred to say, “effective computing system” without first defining it, etc, etc, but I’m not interested in infantile games like that.
Two of Mark’s definitions:
http://www.goodmath.org/blog/2009/05/15/you-cant-write-that-number-in-fact-you-cant-write-most-numbers/
http://www.goodmath.org/blog/2014/05/26/you-cant-even-describe-most-numbers/
Mine: A real number having a finite representation;
There is a definition in a given formal system that can be written down with a finite number of symbols, and which precisely defines the entire expansion of that number (to a given base).
A real number not having a finite representation;
There is no definition in any formal system that can be written down with a finite number of symbols, and which precisely defines the entire expansion of that number (to a given base).
Why is Chaitin’s number irrelevant? Several reasons, here’s two.
1) because for the umpteenth +1 time, I asked for a proof there exists real numbers with no finite representation within ZF set theory. You simply assert that Chaitin’s number can be defined within ZF and expect everyone to simply take your word for it. I don’t. The only entities in ZF are sets; Chaitin’s number is defined in terms of Turing machines that stop or don’t stop. But you provide no reason why I should believe that ZF can refer totally WITHIN itself to Turing machines stopping or not stopping.
2) According to you, Chaitin’s number “exists” without any finite representation, but the only evidence you provide for that is Chaitin’s definition, which is such that the number cannot be completely derived from that definition, since it is defined in terms of halting probability. From that you conclude there cannot be any finite representation, since that would solve the halting problem. But that does not mean that there cannot be an alternative finite definition of the number, and which makes no reference to halting probability. Since you haven’t yet proven that there is any real number that has no finite representation, then you cannot assume that there is no such finite definition. So one such finite definition can be the definition of the same decimal expansion as Chaitin’s number, but you have no way of proving that it is Chaitin’s number, since you can’t deduce the digits of
Chaitin’s number indefinitely, but you could for the alternative definition – and so you still can’t solve the halting problem. So you still haven’t proved that there exists a real number that has no finite representation.
So, if you are indeed referring to terminating expansions in some whole number base, the framework of the argument is as follows: Numbers with that have terminating expansions are easily shown to be rational numbers, and using accepted definitions of the real numbers (as a complete ordered field based on the ZF axiom system) we can prove the existence of irrational numbers. Every irrational number must have a nonterminating expansion because otherwise it would be rational and that is a contradiction.
Need I elaborate on this basic framework, and to what end?
Want to know the difference? Because you can look up effective computing systems (or recursive computing systems), and find the definition. You can read a dozen different textbooks, and completely understand exactly what I mean, and what Chaitin’s constant means. As I explained clearly and in detail: the phrase “infinite representation” can have multiple meanings, and I carefully gave you a list of options. (Which, I will note, you ignored and gave your own, less precise definition.)
Chaitin’s Ω can absolutely be determined from that definition. Once again, you’re not understanding a mathematical definition. Chaitin’s Ω defines a halting probability; it isn’t defined by a halting probability. It’s defined by a simple fact: given a computing system
and a program 
, does 
halt?
Of course, you’ve got a convenient way to wiggle out of that. I give you a number which meets your requirements. But you sneer and say it doesn’t count, because I’m only allowed to use pure ZF, which consists of nothing but sets. But that kind of weaseling gives you a universal out. Real numbers aren’t part of pure ZF – they’re part of a construction on top of it. The concept of a decimal expansion isn’t part of pure ZF. Anything I can produce will, necessarily, depend on constructions built on top of ZF.
I can’t talk about real numbers in pure ZFC set theory, because real numbers aren’t a concept there. Real numbers are part of a mathematical theory constructed using ZFC set theory. I can talk about them using set theory, because the theory of real numbers is built using ZFC as a foundation. The real numbers are a set – and I can prove that using ZFC, but not only ZFC.
To meaningfully define the real numbers, I need to start by defining the natural numbers. I can do that by defining their mathematical properties using the axioms of Peano arithmetic written in first order predicate logic, and then I can show that there is a model for that theory in sets using ZFC. Once I’ve done that, I can use all of the axioms of ZFC to construct sets of natural numbers and do proofs over those sets using the axioms of infinity, comprehension, and induction. That gives me a valid ZFC-backed theory of the natural numbers. Once I’ve done that, I can construct a theory of integers using a set of axioms, and show that there’s a model for that theory using ZFC and sets of natural numbers. Once I’ve done that, I can built sets and proofs about those sets using the axioms of ZFC like comprehension, infinity, and induction. Then I’ve got a valid ZFC-based theory of the integers. I can then define the rational numbers using a series of axioms, and show that there’s a model for those using ZFC and sets of integers. That gives me a valid ZFC-based theory of the rational numbers. Then I can define a set of axioms defining the real numbers, and show that there’s a valid model for those using ZFC and sets of rational numbers. That gives me the theory of the real numbers.
I need all of that construction before I can really talk about the set of the real numbers. That doesn’t get to the necessary background that’s needed to talk about decimal representations and digit expansions.
The thing is, this is what math is about. It’s about building stacks of intricate and carefully defined structures. You start from a very simple base, and build the world on top of it.
ZFC isn’t a great theory because it includes everything. It’s a great theory because it provides a platform and a set of building blocks that you can use to construct almost anything.
As I said in the previous post: I can define recursive function theory, but it’s not something that can be defined in a blog post. It’s something that requires a textbook. Likewise for just about any interesting thing. I can’t define a transcendental number in pure set theory. I can’t define π in pure set theory, because numbers don’t exist in pure set theory. But I can build numbers using set theory.
I can define Chaitin’s numbers, because I have set theory as a foundation. I can use set theory to define natural number theory, and then natural number theory to define recursion function theory. First order predicate logic defines the rules, and set theory provides the model. That gives me the objects I need to talk about computation. Using set theory, I can define objects and sets using ZFC axioms. Look at the definition of Ω: it’s a valid set theoretic construction, built on the axioms of comprehension, infinity, and induction, operating over the objects of recursive function theory.
I am a mathematician, not that it matters. Mark’s arguments and requests are sound. But forget them for a moment. I will happily acquiesce to your request if you please define “finite representation”.
For example, by “finite representation” do you mean “terminating decimal expansion”? If so, I can easily demonstrate the existence of such numbers.
Mark, re your comment of January 26, 2018 at 5:00 pm
I never used the term “infinite representation”. That is why I did not define it, and why I ignored your definitions of it. The term I actually used was “finite representation”, whose meaning is perfectly clear to you, as used in your blogs
http://www.goodmath.org/blog/2009/05/15/you-cant-write-that-number-in-fact-you-cant-write-most-numbers/ and
http://www.goodmath.org/blog/2014/05/26/you-cant-even-describe-most-numbers/
You say:
“Chaitin’s Ω can absolutely be determined from that definition.”
No, it can’t. But there can be an assumptive notion that the Chaitin number “exists” if one takes together both that definition and the assumption that for any Turing machine/program, there “exists” a Platonist “true” or “false” value for whether it halts, and which is completely independent of whether there exists any finite method that can determine if that Turing machine/program halts. That is very different to asserting that the Chaitin definition of itself is sufficient to determine a specific number – the definition itself without that assumption does not give a determination of any specific number.
Let’s pretend for a moment that your argument that Chaitin’s number does actually provide an example of a real number that has no finite representation. Then your “proof” that there “exists” a real number for which there is no finite definition that can determine its value relies on the assumption that there “exists” “true” and “false” values for which there are no finite definitions that can determine such values. Don’t complain if anyone rejects that argument on the grounds that it is absurdly circular.
But, anyway, I don’t need to point out the circularity of the argument. I only need to reiterate the point of my previous comment that you simply ignored. Just because you have an assumption together with Chaitin’s definition that gives you an assumed number R that you cannot determine by any finite method, that does not mean that there is no alternative finite definition B that gives that assumed number R, where the definition B makes no mention of Turing machines or computer programs. Knowing the definition B does not enable you to solve the halting problem, since there is no method of determining if any given definition (including B) is a definition that gives the assumed number R. Hence there is no proof that R does not have a finite representation.
It’s nice to see that at last you admit that, actually, it’s better to use all sorts of other stuff besides ZF set theory to do all sorts of math.
Your problem in this entire discussion is that you don’t understand any of the things that you’re talking about.
You specifically challenged me to, using ZFC set theory, prove that there exists a real number with no finite representation.
I did that.
You’re now quibbling with an objection that amounts to “I don’t know what it means to define something in ZFC set theory”.
I’m going to repeat this one last time.
The whole argument of the post that started this reply thread is: in mathematics, we use formal notation, formal language, and formal reasoning for a reason: because that kind of precision is crucial to doing math.
ZFC is a foundation on which we define other theories of math. It’s a key part of all of modern mathematics. It’s not all of math: it’s the foundation of all of math.
You challenged me to produce a number with no finite representation using ZFC set theory.
How does a mathematician define something like a number with no specific representation?
They provide a set-theoretic definition that precisely specifies the number they’re talking about.
How do they know that the thing they defined actually exists? Because they define it in ways that are valid within the foundational axioms of the system of mathematics.
How did I define Chaitin’s Ω?
I started by talking about a recursive (or effective) computing system. That’s a construct well-defined using the foundation of set theory.
Then I defined a set of values:
. Halting is a concept defined in the theory of computation. It’s a predicate. Using simple ZFC, I can define a set using a predicate, according to the axiom of specification. That set – 
is absolutely a valid, well-defined set under ZFC set theory. And an expression that sums over the elements of a set of integers? Absolutely valid under ZFC set theory.
But you’re playing a game by trying to add new rules – new rules which you neither stated nor defined. Under ZFC set theory, Chaitin’s number exists. Mathematically, Chaitin’s number exists.
Your argument against it is:
But the whole point of formal mathematics is that it defines exactly what you can and can’t do: whot, under a given set of definitions, exists; what, under a given set of definitions is provable.
We’re talking in terms of the mathematics based on ZFC set theory. What defines whether or not something exists is the axioms of ZFC, and the constructs that we build using those axioms. The whole point of that formalism is to address exactly this argument: there’s no room for opinion here. The mathematical foundations and the mathematical reasoning process tell us exactly what we need to know, without a scrap of ambiguity. If we’re talking about mathematics? Chaitin’s number exists.
And one last quibble:
I don’t admit anything remotely like “It’s better to use all sorts of other stuff besides ZF set theory”. What I said in that previous comment, which you’re trying to twist here, is that ZFC is the toolbox that we use to built all of the theories of mathematics that we use every day. ZFC isn’t all of mathematics: it’s the foundation that pretty much all of modern mathematics is built on. When I’m doing number theory, I haven’t stopped doing ZFC: I’m working in a theory who’s model and underpinnings are defined with ZFC. ZFC is still a fundamental part of it.
When I’m doing the theory of computation, whether I’m doing it via the mechanistic version, or via recursion function theory, I haven’t stopped doing ZFC set theory. I’m still working in a theory that’s built using ZFC as a foundation, and I’m still using ZFC every step of the way.
I’m not doing something besides ZFC. I’m doing something built with ZFC.
Mark, you say of me: “Your problem in this entire discussion is that you don’t understand any of the things that you’re talking about.””
When you have to resort to hyperbole, an intelligent reader knows that it doesn’t actually make any useful contribution to the debate, and can see that the notion that I don’t understand any of what I’m talking about is ridiculous.
You seem to think that formal systems cannot include any assumptions. But of course they can, in fact they must, otherwise there could be no formal axioms. And of course that means that there isn’t any way of proving that the axioms of your formal systems are indubitably “correct”.
You keep banging on about your chosen formal systems as if your chosen formal systems are the only possible “correct” formal systems, saying: “there is no room for opinion”. But you can’t prove that the axioms of your chosen formal systems are the “right” ones – and so there is no reason why anyone should accept your formal axioms as the “right” ones – and hence there is no reason to accept your chosen formal systems as the “right” ones. You can say that I don’t understand anything of what I’m talking about – but the evidence of who understands what they are taking about lie within the words on this page.
You started off by insisting on ZF set theory. Fine. But now you are talking about all sorts of other stuff and simply asserting that it can all be formalised. But doing that isn’t really any different to talking informally, because now no-one can be sure what assumptive axioms and rules of inference you would be using if it was all put in strict formal terms.
Of course you can use your chosen formal systems and obtain the results you desire. And we can accept that you will include whatever assumptions you make as axioms of your formal systems. But that does not mean that we have to accept those axiomatic assumptions as some sort of gospel that may not be challenged. And it does not mean that we have accept those axiomatic assumptions if they lead to a circular argument. Accepting Platonist assumptions that are assumptions of the “existence” of mathematical entities independently of any finite definition is akin to a faith based belief in a deity – as is assuming that all propositions have a definite “true” or “false” value independent of any means of determining such values.
But the above presumes that your claim is correct – that your formal systems can “prove” the “existence” of a number that has no finite representation. But the fact is that all that a formal system can prove is that the symbol sequences that is Chaitin’s definition – i.e., that the finite representation of Chaitin’s definition in that formal system satisfies the formal requirements in that formal system for “existence” – that is, that it satisfies the definition of a real number in that system.
You are asking me to accept that you can have a formal system that can say, in effect, where Omega is Chaitin’s definition in that system:
“Omega is a real number, and there exists no y such that y = Omega, where y is a finite symbol sequence for a real number (in this system).”
But that would be absurd, since Omega is a symbol sequence of that system. The idea that a formal system can say something about the “existence” of a number that “exists” outside of that formal system is absurd. Of course, people can attach interpretations onto the statements of formal systems, but here we are dismissing such interpretations, since this page is about why formality is important in maths.
Finally, you brazenly claim that you have proved that there exists a real number with no finite representation. But you haven’t, and you completely ignored the key point that I have already pointed out twice – which is that the definition of Chaitin’s number does not prove that there does not exist an alternative definition of that number that makes no reference to Turing machines/programs, and hence cannot be used to solve the halting problem, since there is no way of identifying that number as the Chaitin number.
You didn’t even refer to either instance of the two times I made that argument, so the presumption must be that you do not find any flaw in that argument.
Gallop, gallop, gallop. As I said, I’m done with this. You’re welcome to run off and declare victory. Goodbye.
@James: you wrote:
“Let me start by stating that I completely accept that the diagonal proof does indeed prove that there can be no enumeration of the real numbers in the same language as those real numbers.”
Would you formalise the statement “there can be no enumeration of the real numbers in the same language as those real numbers”?
When I said that I accept that “there can be no enumeration of the real numbers in the same language as those real numbers”, I was referring to diagonal proofs that I have encountered, noting that fully formal proofs only prove the case for when the natural numbers and the real numbers are in the same formal language.
But what you are doing is that instead of actually supplying a fully formal proof that the diagonal proof is correct regardless of what languages the natural numbers and the real numbers belong to, you are asking me to provide a formal proof that that is not the case.
That’s not how mathematics proceeds, and it is not how it should proceed. When someone makes a claim that a mathematical statement is correct, the onus is on them to prove it with sufficient formality, not for someone else to prove the contrary.