As you may have noticed, E. E. Escultura has shown up in the comments to this blog. In one comment, he made an interesting (but unsupported) claim, and I thought it was worth promoting up to a proper discussion of its own, rather than letting it rage in the comments of an unrelated post.
What he said was:
You really have no choice friends. The real number system is ill-defined, does not exist, because its field axioms are inconsistent!!!
This is a really bizarre claim. The field axioms are inconsistent?
I’ll run through a quick review, because I know that many/most people don’t have the field axioms memorized. But the field axioms are, basically, an extremely simple set of rules describing the behavior of an algebraic structure. The real numbers are the canonical example of a field, but you can define other fields; for example, the rational numbers form a field; if you allow the values to be a class rather than a set, the surreal numbers form a field.
So: a field is a collection of values F with two operations, “+” and “*”, such that:
- Closure: ∀ a, b ∈ F: a + b in F ∧ a * b ∈ f
- Associativity: ∀ a, b, c ∈ F: a + (b + c) = (a + b) + c ∧ a * (b * c) = (a * b) * c
- Commutativity: ∀ a, b ∈ F: a + b = b + a ∧ a * b = b * a
- Identity: there exist distinct elements 0 and 1 in F such that ∀ a ∈ F: a + 0 = a, ∀ b ∈ F: b*1=b
- Additive inverses: ∀ a ∈ F, there exists an additive inverse -a ∈ F such that a + -a = 0.
- Multiplicative Inverse: For all a ∈ F where a != 0, there a multiplicative inverse a-1 such that a * a-1 = 1.
- Distributivity: ∀ a, b, c ∈ F: a * (b+c) = (a*b) + (a*c)
So, our friend Professor Escultura claims that this set of axioms is inconsistent, and that therefore the real numbers are ill-defined. One of the things that makes the field axioms so beautiful is how simple they are. They’re a nice, minimal illustration of how we expect numbers to behave.
So, Professor Escultura: to claim that that the field axioms are inconsistent, what you’re saying is that this set of axioms leads to an inevitable contradiction. So, what exactly about the field axioms is inconsistent? Where’s the contradiction?
I am trying to read “On Numbers and Games” 2nd ed. Could you please revisit division of surreal numbers? The first comment in your post http://scienceblogs.com/goodmath/2007/04/surreal_division_a_weak_post_1.php asked for code to describe surreal division. That would be wonderful!
Reply to Mark.
12 of the field axioms are listed in Royden’s Real Analysis, pp. 31 – 32. One of them is the trichotomy axiom to which Brouwer and I constructed counterexamples. EEE
Reply to MarkCC
What I call the field axioms are these 7 axioms plus the order, completeness, transitivity, and multiplicative and additive axioms. EEE
Rely to Mark CC on his claim that my claims are unsupported.
1) All my claims here are fully estalished right here or supported by original sources published by per reviewed international publications that I have identified here.
2) Therefore, either Mark has blurred vision or he does not understand the original sources which is understandable since the level of mathematics there is above non-mathematicians.
Cheers,
E. E. Escultura
It’s worth mentioning that the field axioms have very important and simple models (and are therefore consistent), namely finite fields ; in particular the very simple sets ${ 0, ldots, p-1}$ for prime numbers $p$ (with the operations being the usual integer operations modulo $p$).
But I suspect the silly objection is more about complete, Archimedean, ordered fields (of which there is just one, the reals). I know a few reasonable problems with the reals (say, from a constructivist’s point of view), but consistency is simply not the problem…
Btw, <a href="http://www.mathoverflow.net" hasn't had any logic cranks in a while, maybe you can reduce your load by sending him there 😉
The field axioms and your model are distinct mathematical spaces; therefore, you cannot make any conclusion in one based on the other. Only cranks do not realize this. EEE
I advise you to start reading elementary math books and thinking about mathematics. It will be good for you.
Just don’t start with advanced ones, but with more elementary. Maybe you can grasp the square root concept, and then the imaginary number concept, who knows.
If I were you, I would start with some author with talk a lot about limits, derivatives, integrals, Cantor’s transfinite numbers, the logic behind mathematics, axiomatic geometry, Fermat’s Last Theorem, Gödel’s work and Number Theory, all subjects you openly reject.
A good author who comes to my mind is Hilbert. He worked in all those fields. You can learn a lot from him.
(Yes, Hilbert published, too, and he also contradicts everything yours).
I have checked this name and found no evidence at all that this person is a mathematician (published). What do you call a nonmathematician who pretends to know and expounds on mathematics? Crank, isn’t it? EEE
I checked Escultura’s name and found no evidence at all that he works as a linguist. What do you call a non-linguist who pretends to know and expounds on language?
Great logic.
Every post you write is more stupid.
I think independently of books and other writings the reason I can make a critique of them. In short, I am creative and original. EEE
Reply to John:
You must be seeing things.
Reply to MarkCC
My thought is not bound by books, authors, etc. alone. I have originality and creativity that allows me to make a critique of existing mathematics and contribute to it. Being bound by them allows only route learning and manipulation of symbols which are not be sufficient to make one a mathematician. EEE
Can you define precisely what you mean by a “mathematical space”? It seems to be like no other mathematical definition of “space” I’ve ever seen. Everytime someone demolishes one of your “proofs” you simply declare that one of the tools they’ve used lives in a different “mathematical space” and cannot be mixed. It’s a lousy trick, and needless to say this kind of nonsense has no place in real mathematics, where many advances have been made by unifying seemingly disparate fields.
And it’s particularly ironic that you won’t allow Peter to discuss a finite field model when your entire proof that (0.999… != 1) seems to consist of the statement (apples != oranges)
I think Mr. Escultura is in a “different space” from the rest of people XD
A mathematical space is a system of concepts including symbols and operations well defined by a set of consistent axioms. This is an example of creative and original work the reason you have not seen this before. EEE
Reply to John. Glad to see you admit that you are an impostor in mathematics and turn to linguistics instead.
Reply to Andy. See the definition below.
The problem is you depend on what you have seen or heard and you do not do mathematics. That is why you cannot even quote me right.
Cheers,
EEE
Oh, now you have proven I admit to be an impostor in mathematics!
Yea, a proof so rigorous as your “proof” about FLT.
Wow, all your proofs are full of rigor.
Have you visited your psychiatrist lately? Stopped taking the medication?
Surely it doesn’t matter whether or not he’s a published mathematician?
Is his conclusion, or the conclusion that he agrees with, correct, given the axioms that he chose when he made his “field”, I think we’re calling it? If so, then it doesn’t matter if he’s published or not, he is correct.
If we only let published mathematicians publish, we’d run out pretty quickly!
And no, I’m not a published mathematician.
ES
A mathematical space consists of objects including symbols and operations well defined by a set of axioms. EEE
Reply to John
An impostor in math is one who expounds on mathematics without being a mathematician (published) and does not admit it. Such person ought to see a psychiatrist. EEE
Reply to Andy
Mathematical space, mathematical system and axiomatic system are equivalent. They are built on consistent premises or axioms. Topologists and physicists generally prefer “space” and algebraists system”. However, distinct mathematical systems are independent and have nothing to do with each other since each is defined solely by its axioms and you cannot prove a proposition in one using arguments in another. That would be like playing a game of chess and taking a piece on the checker board. You need to expand your horizons, Andy, and learn new things.
Reply to Andy M
A mathematical space is well defined by a set of consistent premises or axioms and distinct mathematical spaces are well defined by distinct sets of axioms. Therefore, they are independent and have nothing to do with each other. Consequently, any concept in one is nonsense in the other and any argument in one is not valid in the other. Is this clear, Andy?
Reply to Andy
A mathematical space is mathematics generated and defined by a consistent set of axioms.
Reply to Andy
The same thing as axiomatic system. It is well defined only by its basic premises or axioms.
Reply to Peter,
Your claim is based on the premise that finite fields are consistent. – EEE
0*1=1*0=0*0=0+0=1+1=0
1+0=0+1=1*1=1
What is inconsistent in that?
Reply to Peter
I suspect you have not understood my posts. I never said anything inconsistent with your post. Or, maybe, you are just trying to show us what you know. EEE
Reply to sineram
The inconsistency in the field axioms lies in the trichotomy axiom to which Brouwer and I constructed counterexamples independently.
Reply to scineram
Is this all that you have in a finite field? State your axioms first and define the operation *.
Reply to Peter. A counter example is sufficient to prove inconsistency of a mathematical space and Brouwer and I constructed a counterexample each to the trichotomy axiom of the real number system independently.
Cheers.
E. E. Escultura
I think you’ve made a small type in axiom 1.
a*b in F, not a*b in f
It also may be more clear to split the “^” over two lines, but that is simply a stylistic preference.
Perhaps what Prof E doesn’t like is the fact that the two operations have all the same properties except one, namely that the multiplicative identity has an exception while the additive doesn’t. I think most people accept that for what it is since it is still internally consistent, even if it does break the symmetry.
The symmetry is already broken by the law of distributivity.
Note that distributivity implies that 0*a = 0 for any a, so if 0 had a multiplicative inverse, it would follow that 0 = 1. (So without the exception, the axioms would indeed be inconsistent.)
Actually, for some fields the distributive law still works if you swap operations. Note that this doesn’t contradict distributivity as an axiom; it’s merely a subclass.
You’re right, it does work for F_2 (i.e. the set {0, 1} with the integer operations modulo 2), but it doesn’t for any other field, does it? (a + (1 * 1) = (a + 1) * (a + 1) implies a = -1 or a = 0 for any a.)
Well, “multiplication” and “division” also have to be defined 🙂 If you’re using AND and OR constructs for mult/div you can get fields as well, for example.
Sorry, that should be “multiplication” and “addition”.
No, that is not my objection. The counterexamples to the trichotomy axiom that Brouwer and I constrcted independently reveals the inconsistency of the field axioms. EEE
I call field axioms the 12 axioms in Royden’s real analysis plus the order axioms. EEE
That is not my objection to the real number system. My objection is that its axioms are inconsistent. EEE
Reply to Bruce
What I object to is the application of operations in the real number system such as + and * to numbers that do not belong to it such as d* which is neither a real number nor a decimal. Please see my reply to Andy.
Pardon my ignorance here, but is infinity part of F? And if so does infinity – infinity = 0? That would be an exception to the additive identity.
First, don’t confuse a field with the set of real numbers. The field axioms don’t specifically define the real numbers; they define the behavior of a structured set with two compatible operations. The real numbers are the canonical example of a field, but they’re not the only one. You can define a field with as little as two values.
Second: Infinity isn’t a number. So no, it’s not part of F.
Thanks, Mark.
Reminder for MarkCC.
The real number system is supposedly a complete ordered field which is neither.
Reply to MarkCC
Yes, the real number system is distinct from its axioms, the field axioms. But the field axiom is supposedly a complete ordered field where the ordering is by “<".
I feel this VERY strange. What exactly here is inconsistent indeed?
Mark, why are you using the “^” symbol here? When “^” gets used in a formula like ^^pqr=^p^qr, or in infix notation (p^q)^r=p^(q^r), “^” functions as a logical operation on variables (or constants). Here, however, in say the associativity axiom you don’t have a logical operation on (a*b)*c=a*(b*c) and (a+b)+c=a+(b+c). Nor are (a*b)*c=a*(b*c) and (a+b)+c=a+(b+c) logical constants or variables. If we had a logical operation on (a*b)*c=a*(b*c) and (a+b)+c=a+(b+c), in principle we could use just one of them instead of both of them.
Boolean Algebras form a field don’t they? So, if *all* fields are inconsistent, then the structure of classical logic is inconsistent also.
In first order logic, the big version of the wedge ^ means “AND”. Given two logical statements, P, Q, the statement “P ^ Q” asserts that “P AND Q”. Mark’s usage is fine.
For another example, you can see some usages of ^ in the following page, defining ZFC set theory:
http://en.wikipedia.org/wiki/Zfc
Not to say that some authors don’t use it the way you’ve indicated, but there still exists a difference between the conjunction of two statements (which is one proposition) and two statements like the above. If I talk about Kpq (p^q) in logic, I’ve talked about the conjunction of two statements, which is one proposition. If I talk about “p”, and I talk about “q”, I talk about two propositions. The “and” in the last sentence isn’t an operator. It more means “also”, though English doesn’t express this all that well in my opinion.
Although, “p and q” comes closest to expressing the meaning of conjunction, Kpq, in logic, conjunction in logic says more than just “p and q”, if construed as meaning that “p is true and q is true”. Half of the 16 standard truth functions “Z” can get construed as saying “p is true and q is true.” That is, if we have “p is true, q is true also as hypotheses, and infer Zpq is true.”
If p is false, and q is false, then Kpq is false. Is associativity for “*” or “+” capable of working out as false in the case of the field axioms? If not, then (a*b)*c=a*(b*c)^(a+b)+c=a+(b+c) doesn’t have the same meaning as conjunction does in logic when dealing with propositions with variables, since in logic wherever we have a variable, we may obtain a truth value of false.
(a*b)*c=a*(b*c) and (a+b)+c=a+(b+c) also aren’t constants. They qualify as equalities.
I take that back. I guess (a*b)*c=a*(b*c) and (a+b)+c=a+(b+c) qualify as constants for the field axioms, but they don’t qualify as constants *like* “a”, “b”, and “c”. Still, do the axioms mean to talk about the conjunction of the two propositions (a*b)*c=a*(b*c) and (a+b)+c=a+(b+c) or that both work out as true?
I was wrong about Boolean Algebras. People write of Boolean *rings* not fields.
Reply to Doug Spoonwood
The inconsistency is shown by the counterexamples to the trichotomy axiom, one of the axioms of the real number system.
Hi,
I also do not know why the professor is claiming the theory of real numbers is inconsistent. Now I find this hard because the theory of real closed fields is founded on the axioms of the theory of fields.
The theory of real closed field has some added axioms on top of what has been listed here. If this is inconsistent how could the real closed field be decidable, whose initial axioms are that of the theory of fields?
LPC
See my reply below – E. E. Escultura
P.S. The inconsistency of the real number system resolves all the questions you have raised. Anyway, glad to see someone from our kind after a long long time – EEE
Reply to LPC
By the field axioms I mean those listed on pp. 31 – 32 of Royden’s Real Analysis (MacMillan). One of them is the trichotomy axiom to which L. E. J. Brouwer and I constructed counterexamples separately (sources cited elsewhere in related thread). This, alone makes the field axioms inconsistent. Since the real number system is supposed to be a field, it suffers from this inconsistency
Reply to LPC
One of the axioms of the real number system is the trichotomy axiom to which Brouwer and I constructed a counterexample each independently.
I have responded to the comment on the field axioms here but it is missing. Here is my response.
The field axioms are listed in Royden’s Real Analysis, pp. 31 – 32. One of them is the trichotomy axiom that says, given real numbers x, y one and only one of the following holds: x y. L. E. J. Brouwer and I constructed two different counterexamples to them in Benacerraf, P. and Putnam, H. Philosophy of Mathematics, Cambridge University Press: Cambridge, 1985 and Escultura, E. E. The new real number system and discrete computation and calculus, Neural, Parallel and Scientific Computations, 2009, 17, pp. 59 – 84, respectively. This means that the trichotomy axiom is false which makes the field axioms inconsistent. Moreover, the completeness axiom which is a variant of the axiom of choice leads to a contradiction in R^3 known as the Banach-Tarski paradox. The contradiction does not come from this axiom perse but from the use of the universal or existential quantifier on infinite set which is ambiguous.
Banach-Tarski is certainly counterintuitive, but it’s not really a contradiction, nor is it a demonstration of the inconsistency of set theory.
Given an infinite set, like the set of integers, you can divide the set in half – and you end up with two sets that are exactly the same size as the original set.
That’s basically what the Banach-Tarski “paradox” does. In topological terms, a sphere is nothing but a set of points that happen to match a particular set of “nearness” constraints. Since the points in the topological space are an infinite set, you can, of course, divide them into two equal-sized infinite sets.
What the Banach-Tarski proof does is show how to “slice” the infinite into two equal-sized infinite sets that both have the same topological structure as the original.
It’s counter-intuitive until you pick it apart – and then it actually makes perfect sense. There is no contradiction there.
Banach-Tarski is not about topology, but rather geometry. It demonstrates how naive notions of the “volume” of a set need to be refined to what we now call measure theory. Note that the notion of “size” involved in Banach-Tarski which appears to be violated is the volume (not say the cardinality or something like that).
Whatever version you pick Banach-Tarski is a topological contradiction in R^3. EEE
Really, Banach-Tarski does not have to do with topology. But whatever.
Reply to SeanH
Banach-Tarski construction is based on the axiom of choice (or, more broadly, the ambiguity of infinite set). It does not matter where the contradiction arises – in topology, geometry, analysis, etc. – as long as you use these tools, you have a contradiction nevertheless. EEE
Reply to SeanH
Both versions of Banach-Tarski construction that I know are in R^3 which is a topological space.
My reply is in http://scientopia.org/blogs/goodmath/. Good luck. EEE
Well, here’s some of the confusion then. Royden breaks the axioms for real numbers into three groups. On p. 31 are the Field Axioms, on p. 32 are the Axioms of Order and on p. 33 is the Completeness Axiom.
The trichotomy axiom is part of the Axioms of Order–this has nothing whatsoever to do with the Field Axioms. So to be clear: if you have a proof that trichotomy is inconsistent then you have not found an inconsistency in the Field Axioms, rather you have found an inconsistency in the Axioms of Order.
I don’t split them into two groups but if you insist I’ll call their union the axioms of the real number system. They characterize the latter as a complete ordered field. The counterexamples to the trichotomy axiom still make the real number system inconsistent being based on inconsistent set of axioms. EEE
So the natural followup question: what is your reference for the trichotomy axiom being inconsistent with the rest of the real number axioms?
Reply to Huber
My references are: L. E. J. Brouwer’s and my articles in Bennaceraf and Putnam’s Philosophy of Mathematics, Cambridge University Press, and, The new real number system and discrete computation and calculus, Neural, Parallel and Scientific Computation, respectively. EEE
I have responded to the comment on the field axioms several times but they keep disapearing. I, therefore, refer the viewers to Larry Freeman’s website, False Proofs, for my response.
Response to other points raised on this site.
A real number is well-defined if every digit is known or computable. Therefore, only the terinating decimals are well-defined. This is the reason we cannot add or multiply nonterminating decimals. We can only approximate the result. Division of an integer by a prime other than 2 or 5, e.g., 2/7, is ill-defined becaus the result is nonterminating decimal. Moreover, applying any operation in the real number system on the dark number d* is improper, i.e., nonsense, because d* is not a real number. For more on the new real number system see, Escultura, E. E. The new real number system and discrete computation and calculus, J. Neural, Parallel and Scientific Computations, 2009, 17, pp. 59 – 84.
Cheers,E. E. Escultura
You’re confusing a real number with it’s decimal representation. The decimal expansion of a number is its image under some function from R to the set of all sequences in {0,1,2,3,4,5,6,7,8,9}, it is not the same thing as the number itself.
A real number is presently ill-defined because of the inconsistency of the field axioms of the real number system. The decimals, terminating and nonterminating, are now well-defined by the three axioms of the new real number system.
Cheers,
E. E. Escultura
You continue to ignore the fundamental, crucial question. You assert that the field axioms of the real number system are inconsistent. How? Where’s the inconsistency?
This entire discussion started with that question, and you’ve continued to ignore it, in favor of just blindly asserting that it’s true.
The field axioms are one of the most fundamental, foundational rules describing the behavior numbers. You can’t just *say* that they’re inconsistent, and expect everyone to nod their head and agree. You need to *show* why they’re inconsistent.
So why are you refusing to answer that simple question?
I have posted several times here or on links to this blog that the trichotomy axiom is false. L. E. J. Brouer and I have constructed separate counterexamples to them. Brouwer’s counterexample and mine are in Benacerraf, P. and Putnam, H. Philosophy of Mathematics, Cambridge University Press: Cambridge, 1985 and Escultura, E. E. The new real number system and discrete computation and calculus, J. Neural, Parallel and Scientific Computations, 2009, 17, pp. 59 – 84, respectively. Moreover, the Banach-Tarski paradox which is a topological contradiction in R^3 uses the axiom of choice in its construction. The completness axiom of the field axioms is a variant of the axiom of choice.
Cheers,
E. E Escultura
Either MarkCC has blurred vision that he has difficulty reading blog posts or he simply does not know that a counterexample to an axiom of a mathematical system is an inconsistency. BTW intuition is irrelevant to a mathematical system.
There are many things you cannot see on your own blog, MarkCC. May be you simply need to read the posts before yours umpteenth times or, maybe, put on your eye glasses. I have no remedy for you.
What is a real number anyway? EEE
Now we’re getting philosophical…
Please, at the very bottom, below all the comments, post a useable link to your proof that the field axioms are inconsistent. Not a citation, an actual, working link, a website address or something…
That way, we can at least pick apart your ideas using your terminology.
ES
You, too, has blurred vision, ES; my sources are all spelled out in my posts.
What is a real number in your sense anyway? EEE
And that is total, absolute, and utter rubbish.
For example, it claims that the set of well-defined real numbers depends on what notation we use. What makes base-10 special?
We could choose to be like the babylonians, and use base-60. Then 1/3, 1/5, 1/6, 1/12, and 1/15th would all be well-defined. But 1/7th would be ill defined.
We could choose base-7. And then 1/2 would be ill-defined.
Your idea of numbers is completely ill-defined: in your system, no fractions are really well-defined, because by choosing different number bases, you can get completely different sets of numbers. There are *no* fractions that are always defined in your system. And that’s obviously total rubbish – how can the set of well-defined numbers *change* depending on notation?
To understand what I’m saying you need to go back to Hilbert’s time a hundred years ago when he recognized that the concepts of individual thought cannot be the subject of a mathematical space because they are not accessible to others and can neither be studied or analyzed collectively nor axiomatized. His remedy: let the subject matter of a mathematical space be objects in the real world that everyone can look at and study such as letters, symbols, geeometrical figures, etc., subject to consistent premises or axioms. This lack of grasp of these nuances explains the huge controversy that ignited when I pointed out in 1997 that 1 and 0.99… are not equal because they are different objects and to say 1 = 0.99… is akin to the equation apple = orange. Thus, the fractions, decimals, binaries and triadics cannot be built as the same mathematical system regardless of their respective axiomatizations because they are different systems of objects even if there may be isomorphisms between them. The fact that people believed for a long time that `1 = 0.99… reveals paucity or scarcity of critical thinking.
Cheers,
E. E. Escultura
And you ignore the point, once again, in favor of word salad.
Are you seriously arguing that the number 1/3 is sometimes well-defined, and sometimes not, depending on your selection of number base for notation?
I would also like to know how he justifies a definition of “well-defined” by which pi, e, and the square root of 2 are never well-defined.
Either the definitions and axioms should connect to reality—a reality in which the ratio between a circle’s diameter and circumference is a constant that we call pi—or he’s working with arbitrary symbols for their own sake. That’s not inherently a bad thing, but it doesn’t justify Escultura’s claim that his system models reality and the standard real number system doesn’t.
Be specific and state what you think I have ignored. I have responded to all the questions raised here. The problem is you misunderstand my posts. I never argued that “the number 1/3 is sometimes well-defined, and sometimes not, depending on your selection of number base for notation”. Different number bases well define different number systems with their respective sets of axioms. For example, 1/3 base 2 is different from 1/3 base 5. They are different objects. You really need to grasp the meaning of Hilbert’s contribution to mathematics.
Cheers,
E. E. Escultura
Reply to MarkCC
Number systems with different bases and sets of axioms that well define them are distinct. If you have not understood this then you you need to go back to basics. EEE
You are consistently confused, MarkCC. Different number bases define different number systems even if there is isomorphism between them. You need to grasp the essence of my posts on Hilbert if you want to pull ahead of the cranks.
Reply to MarkCC
I don’t think MarkCC really understands what he is posting about. Aside from being unaware of what I have already posted, he raises questions that are irrelevant to the discussion.
‘The fact that people believed for a long time that `1 = 0.99… reveals paucity or scarcity of critical thinking.’
Here I was thinking this was generally accepted that 1 = 0.999… I’ve proven and seen proofs for it in several ways and they all say the same thing. The only arguments against it I’ve ever seen are along the lines of ‘nuh-uh *covers ears*’.
Am I missing something?
1/3 is ill-defined in base 10; it may not be so in other bases. But different bases determine different system of symbols or objects and, hence, different mathematical systems.
With respect to the question by the next blogger, a concept (meaning, symbol or object) is well defined if its existence, behavior or properties and relationship with other concepts are specified by the axioms of the given mathematical system. Note that “existence” is essential because a vacuous concept is inherently contradictory. For example, the concept i = the root of the equation x^2 + 1 = 0 (among the real numbers) is vacuous because there is no such thing. Consequently it leads to the contradictions 1 = 0 and i = 0.
pi and e are well-defined as nonterminating decimals by their respective series expansions and nonterminating decimals are well-defined in the new real number system although they have contained ambiguity (i.e., approximated by certainty, e.g., terminating decimals). Since I am introducting new terms here out of necessity, I refer the bloggers to my original paper on the subject: Escultura, E. E. The new real number system and discrete computation and calculus, J. Neural, Parallel and Scientific Computations, 2009, 17, pp. 59 – 84. (I also refer them to Larry Freeman’s website, False Proofs. All the questions raised here are answered there).
No, I am not working with arbitary symbols for I require them to be well-defined by specific set of axioms. The choice of the axioms are arbitrary depending on what you want your mathematical system to do for you but once they are chosen they become a deductive system, with nor aribrariness.
Cheers,
E. E. Escultura
Sooo… No proof to show 1 doesn’t equal 0.999…? Seriously, if this is something I’ve missed, I want to know the how’s and why’s.
Also…
‘pi and e are well-defined as nonterminating decimals by their respective series expansions and nonterminating decimals are well-defined in the new real number system although they have contained ambiguity (i.e., approximated by certainty, e.g., terminating decimals).’
So infinite series are fine, (even though they will inevitably contain numbers that are ill-defined by this new number system. Seems inevitable to me anyways. Again, I’d love to be proven wrong for both pi and e, since my memory, backed up by a quick google search, suggests it is), but infinite numbers that just happen not to have a series attached to them are ill-defined?
Finally, I fail to see how a number can be ill-defined in one base and well defined in another. Surely that means the overarching system is broken, since there’s no consistency in doing something so simple as changing base.
E.E. Escultura,
You have a point when you write “he recognized that the concepts of individual thought cannot be the subject of a mathematical space because they are not accessible to others and can neither be studied or analyzed collectively nor axiomatized. His remedy: let the subject matter of a mathematical space be objects in the real world that everyone can look at and study such as letters, symbols, geeometrical figures, etc., subject to consistent premises or axioms. ”
“But different bases determine different system of symbols or objects and, hence, different mathematical systems.”
Then 2 in base ten doesn’t equal 10 in base two. 5 in base six doesn’t equal 12 in base three. 15 in base twelve doesn’t equal 17 in base ten. In other words, by stipulating this, there exist different *natural numbers* in every base system, not just different rational numbers. How we have different rational numbers comes as difficult enough to explicate. How do we have different *natural numbers* in every base system? How does four slashes like this “\\” in a notation where we only use slashes for positive natural numbers on a page differ *in meaning* from the Hindu-Arabic numeral “4”? How does “4” refer to a different object than “\\”? How does someone say recording the instances of four customers doing business with slashes for each new customer differ from someone who writes “1”, “2”, “3”, “4”? You’ll effectively need to answer those questions for your ideas to have credibility. So, how do you reply?
Show me a proof that 1 = 0.99… and I’ll point to you where the flaw is.
Cheers,
E. E. Escultura
Well – here’s one for you.
Take 1, and divide it by three. By the field axioms, that must be possible. In decimal notation, what’s the result?
0.3333333….
Now, multiply that by three.
0.3333333….. * 3 = 0.99999999
So – either 0.99999… = 1, or else multiplication and division are inconsistent.
Alternatively, you can say that in your system, 1/3 is ill-defined, because it’s a non-terminating number. But if that’s the case, then 0.9999…. is also ill-defined. And if it’s ill-defined, then it’s meaningless to talk about what it does or does not equal.
Alternately, there’s the basic…
x = 0.999…
10x = 9.999…
10x – x = 9
9x = 9
x = 1
Or…
0.9 = 1 – (0.1^1)
0.99 = 1 – (0.1^2)
…
0.999… = 1 – (0.1^inf)
0.1^inf = 0
0.999… = 1
I’m sure there was at least one more that was shown to me once. My memory is terrible. Anyways, there’s three proofs.
Also, (I realised during a very boring hour or two at work, so this might extrapolating a little too far, I certainly hope so) in an extension to Doug’s statements, it would appear in Escultura’s system, the number 3 in base 4 is different to the number 3 in base 5, so even when using identical symbols meaning identical things, they apparently are totally different? All we’re doing is still using a different numbering system, just like previously.
You need to consider what .999… actually means. It is not an arbitrary symbol open to interpretation it has a very precise definition. That definition being the limit as N goes to infinity of the sum from k=1 to N of 9/(10^k), which is clearly equal to 1.
If you have a different definition of .999… that’s fine but it’s not the generally accepted definition so you should define it, otherwise your claim that .999…≠1 is gibberish.
Reply to Mechanical
Mathematics has nothing to do with belief, acceptance, etc.
It is built on correct reasoning based on consistent premises or axioms. What others have said must be examined if it meets these requriements and not simply quoted. EEE
I’ve seen a proof that 1 = 0.999… that our friend E.E. Escultura himself wrote on the comments page of a different blog.
He promptly ignored that proof.
I do not know why.
ES
Reply to Mechanical
State at least one proof of the statement 1 = 0.99… that you know and I’ll point out what is wrong with it.
Reply to MarkCC
I’m not talking about notations. I’m talking about mathematical objects or concepts and the axioms that well define them.
> applying any operation in the real number system on the dark number d* is
> improper, i.e., nonsense, because d* is not a real number
and yet you use it in your “counter-examples” to FLT, which of course is formulated purely in terms of integers. Further, you apply the standard rules of arithmetic to it to get those counter-examples. Seems like it’s one rule for you and another for everybody else when it comes to d* – or is it just that any operation is allowed as long as it’s not being used to prove d* == 0 ?
My counterexamples to FLT are not real numbers but new real numbers, specifically, new integers, because the real number system is ill defined its axioms being inconsistent as I have explained many times which means that FLT is not well defined in the real number system. EEE
FLT deals only with integers. Do you also think that the (old) integers are ill defined?
Reply to Sean
Yes, the real number system including the old integers are ill-defined. That is why I built the new real number system and its integers, reformulated FLT in it and disproved it. EEE
So what you have disproven is a reformulation of FLT in a seperate number system? So not, in fact, FLT? Brilliant…
ES
Reply to MarkCC
There is something wrong with your equation (o.999…)*33 = o.99…9 because the left side is nonterminating but the right side is terminating; they are not equal. EEE
Reply to E.S
Yes, I disproved the reformulated FLT (in the new real number system) because the original formulation in the real number system is nonsense the latter being inconsistent and nonsense, too.
Aren’t all the digits of 1/3 computable? Seriously, they’re all 3’s. Doesn’t this make it “well-defined” according to you?
Nonterminating decimals are ill defined in the real number system even if the digitss are known because you cannot applytto them its additive and multiplicative operations. try for instance adding .33… and sqrt2 and write the exact answer. EEE
Above you said:
“A real number is well-defined if every digit is known or computable.”
But here you say
“Nonterminating decimals are ill defined in the real number system even if the digitss are known.”
This confuses me.
Reply to SeanH
Nonterminating decimals are ill defined in the sense that not all its digits can be computed. That is why you cannot add or multiply with a nonterminating decimal, you can only approximate the result. I call this kind of ambiguity “contained”. EEE
Or, we could begin with something a little easier.
0.333… + 0.333…
Both non-terminating decimals, yet all of their digits are known, and by adding them together we get
0.666…
obviously.
The fact that you happen to pick a non-terminating decimal that we don’t know all the digits of, and then ask us to list all the digits, doesn’t prove your argument at all.
ES
Reply to E, S.
You overlooked a gaping hole in your addition. If you look at the addition table and its extension to decimals you will notice that in adding two decimals you start by adding their last digits. When you have two decimals and at least one of them is nonterminating you cannot even start your addition because addition is not defined on nonterminating decimals. Therefore, the sum of .66… and .666… does not exist in the real number system
It seems we should go back a little farther, before Plato and his discussions about the ideality of geometrical figures. Good luck finding a perfect square, so we can all “analize it collectively”.
Now, to the point. The tirade on Hilbert is irrelevant, because both 1 and 0.99 … are symbols. It says nothing.
Can you (he who was granted critical thinking) explain us why we can mix 5-2 with 3 in an expression (5-2=3) and not (6/2) with 3 in an expression (6/2=3). (6/2 representing the fraction six halves).
I mean, 3 and 6/2 are not the same symbol, but neither are 3 and 5-2. Can you “critically” explain why do you thing you can not mix them? Why are they “different systems”? I can easily think of a system containing them both.
Reply to John
A binary operation such as +, -. x, a/b is a mapping and that mapping is defined by the axioms. In your “mixing”, 5-2 -> 3 and there us nothing wrong with it. EEE
The really scary thing is what happens when you look for articles by Escultura. It turns out that somebody actually publishes his writings (although most of the journals I found were from Elsevier).
Hilbert is not irrelevant here. In fact, Hilbert reminds us that 1 and 0.99… are distinct objects and we cannot right 1 = 0.99… .
Subtraction and division are both binary mappings and 5 – 2 = 6/2 = 3, i.e., the two mappings have the same image. What is wrong with that?
Cheers,
E. E. Escultura
> “Thus, the fractions, decimals, binaries and triadics cannot be built as the same mathematical system regardless of their respective axiomatizations because they are different systems of objects even if there may be isomorphisms between them.”
> Subtraction and division are both binary mappings
Am I missing something?
(6/2) and 3 are different objects, and we can define a map between them (in this case, division). So we can mix them both in the same expression. For example, (6/2) = 3.
Then, 0.33333…. and (1/3) are different objects, and we can define a map between them. Therefore, we cannot mix them both in the same expression. For example, we can not write 0.333… = (1/3).
Or 0.9999… = 1.
Again. Is something missing in your reasoning?
Mnnn, wait. I see your game.
Despite me explicitly specifying that (6/2) should be interpreted as a fraction, you interpreted it as a division. So, when you wrote (6/2)=3, you were thinking in divide(6,2)=3. And with that you have dodged the question gracefully. My fault, wrong example.
Then, what do you think of this:
0 + 0.9999…. = 1
There is a mapping involved ( sum(0,0.999…)=1 ), and you have to admit that we can define maps between ‘different objects’. No problem with an additive map that mix ‘integers’ and ‘infinite decimals’, is it?
As 0 is the additive identity, what can we conclude?
(Note: If you don’t like mapsinvolving ‘different’ objects, what do we do with all those fields of mathematics, like graph theory?)
I interpret 6/2 as division because division is well-defined by my three axioms. Your interpretation is ambiguous unless you well define the fractions as a mathematical system by a set of consistent axioms.
Binary mappings are not necessarily isomorphic, i.e., 1 – 1. Even isomorphism between two math spaces does not mean they are the same. It means only that there is similarity in their structure or behavior WITH RESOECT TO THEIR CORRESPONDING BINARY OPERATIONS ONLY.
There is no gap at all in my reasoning but you need to scruinize it rigorously and combine it with my other statements to establish the links.
Again, 0.99 = 1 is wrong because the objects are distinct.
I wish there were reply icons to every message. It is very difficult to reply to a long string of different messages. I am bound to miss some of them.
At anjy rate, all the questions raised here are answered in the blogs and websites I referred to earlier. They were raised long before.
Cheers,
E. E. Escultura
You can have a correspondence between two distinct mathematical spaces but that does not mean they are the same.
A correspondence between two distinct spaces simply means that they behave the same way with respect to corresponding operations. In a mathematical space you do not simply apply operations. You also make conclusions and prove theorems which are well-defined solely by its axioms.
Incidentally, Goedel’s incompleteness theorems are flawed. Why? Distinct mathematical spaces are well-defined only by their respective axioms. Naturally, a well-defined concept in one need not be well-defined in the other, i.e., nonsense. Moreover, any proof involving mapping from one mathematical space to another is flawed. In Goedel’s incompleteness theorems he employed mapping from the propositional calculus to the integers.
Incidentally, universal rules of inference, e.g., those of mathematical logic, are no good for axiomatic systemss where the truth values are determined by their respecctive axxioms.
In reply to John, fractions, decimals, binaries and base numbers other than 10 are distinct mathematical spaces. In the case of 1 and 0.99…, they are distinct objects and we canot say 1 = 0.99… for that would be like saying apple equals orange which does not make sense.
Cheers,
E. E. Escultura
“Moreover, any proof involving mapping from one mathematical space to another is flawed.”
Why?
I don’t think you understand how mathematics works. You don’t just claim things, the proof is the important bit.
‘that would be like saying apple equals orange which does not make sense’
Ah yes, but you must remember, birds of a feather flock together.
See? I can use unrelated truisms too. Now prove that they’re different. Don’t hide behind fancy words or simply state things that you haven’t proven, or bring random other theorems or concepts into the mix seemingly out of nowhere only to dismiss them, or (as I let you do already, d’oh!) attempt to disprove other proofs, algebraically prove it. If your system is worth anything, you should be able to use it, instead of words, to prove how we’re wrong and show that this system of yours is consistent, useful and functional.
“Moreover, any proof involving mapping from one mathematical space to another is flawed”
Proof it.
Feel free to refer us to a paper. Even one yours.
(I am very surprised that now I can not count the elements of a set, because the elements are in a “different math space” than the integers we use to count them, and “we cannot accept the mapping involving different spaces”).
(Or the area of a triangle in Euclidean space, because the map “area” relates elements of the space “triangles” with the real numbers. Oh, good bye, Geometry).
0.99… and 1 are distinct objects like an apple and an orange and to say that an apple = an orange is clearly nonsense. EEE
I can understand why nonmathematicians cannot understand my posts. They don’t know the basics.
Distinct mathematical systems are well defined solely by their respective axioms. Therefore, they have nothing to do with each other. Consequently, a conclusion in one cannot be proved in the other and any proof involving concepts in both (e.g., when mapping is involved) is flawed. EEE
Now you only need another excuse that explain why mathematicians cannot understand your posts.
Reply to John, Lily, etc.
Mapping between distinct mathematical systems does not make them the same, it only provides correspondence. A well defined concept or symbol in one mathematical system is ill-defined in another. Therefore, a statement in one cannot be proved in another. EEE
The word”mix” is ambiguous. You can have different binary mappings in the same number system as long as they are consistent. What’s wrong with that, Joh?
Reply to John
In the statement 1 = 0.99… we have two distinct objects 1 and 0.99… and this statement is akin to the statement apple= orange. Is this what you missed?
Correction: “right” should be “write” EEE
Only the insecured are scared. I have over 50 scientific papers in a dozen peer reviewed journals and conference proceedings. But I have the patience to engage in discusion or debate on my work so that others can refute or live with it. No one so far has punched a hole in my work.
Cheers,
E. E. Escultura
“I have over 50 scientific papers in a dozen peer reviewed journals and conference proceedings.”
This demonstrates nothing more than how prolific you are.
“No one so far has punched a hole in my work.”
How far underwater do you need to be, before you realize your ship has sunk?
Non-mathematicians (unpublished) do not grasp the significance of publishing in peer reviewed scientific journals but the arbiter of scientific merit is the network of peer-reviewed publications. Unless a paper is refuted in such journals it stands as contribution to mathematics or science. I post on the internet because experts have not found a flaw in my work and it sometimes happens that the layman can see much further than the experts. As I said earlier I want others to debate my work or live with it. I think I started a new era in mathematics and science by initiating such debate. In this era errors and hoaxes cannot last long.
Cheers,
E. E. Escultura
Birds that flock together are still distinctinct.
Distinct mathematical spaces (defined by their respective axioms) are independent. Therefore, you cannot prove a theorem in one mathematical space based the axioms of another.
isomorphism allows you to count in one math space using the objects in another as labels. But this is a different matter from proving a theorem.
Yes, but according to you, you can’t prove anything anyway, because you aren’t allowed to use logic…
Did you see my ship sink? Where? You might be seeing things. EEE
Sorry, some of my replies have been detached from the questions.
In response to Mark’s last post: You keep misquoting me. EEE
Reply to MakkCC. You keep distorting my statements. I think you need to brush up on English. My logic or rules of inference are well defined only by the axioms of the given mathematical system. EEE
Reply to bibliovore
This is sourgraping. To sink me down a peer should should refute my work and I’m still there vigorously sailing.
How do you explain that each base system has a different set of natural numbers?
What we call natural numbers are the integers of the base 10 system which are isomorphic to the natural numbers developed by Peano.
Cheers,
E. E. Escultura
What is the isomorphism?
Since you didn’t answer it, I’ll ask again “How do you explain that EACH BASE SYSTEM has a different set of natural numbers?” I do consider the recording of events, such as a customer making a purchase, using slashes as involving natural numbers. The base system isn’t base ten. If happens in unary. If I have six customers, I would call that “six” a natural number. In other words, I call natural numbers something other than the integers of base 10 system, and I feel sure most other people would refer to those as natural numbers also. So, I’ll ask again…
“How do you explain that EACH BASE SYSTEM has a different set of natural numbers?”
1/3 is well defined in the system of fractions with appropriate axioms. It is not a decimal and, naturally, it is not well defined in the system of decimals.
You cannot be sloppy in reading mathematical statements.
Cheers,
E. E. Escultura
You’re claiming that you’ve got a valid definition of real numbers. But you keep avoiding the fact that your definition is rubbish, by weaseling your way around and avoiding all of the problems with it.
If you want division to be well-defined, you need to have multiplicative inverses. You don’t.
You claim things like “1/3” is well-defined in the system of fractions, and pretend that that means that you don’t have a problem with things like division by three. But you’ve also claimed that you can’t crossover between different axiomatic systems – so how do you define division by three, without using fractions (because they’re not defined in your system), and without multiplicative inverses, and without having any well-defined value for 1/3?
Even your question is vague. If you mean “… each base system defines a different system of numbers?” I can answer: each base system consists of differennt system of objects. EEE
Doug Spoonwood
What are natural numbers anyway? What I’m saying is: different base systems have different objects.
Mathematical logic does not apply to mathematical spaces or axiomatic systems because it has nothing to do with their axioms that well define them. I know mathematics very well because I do it everyday.
This is one of the most bizarre statements that I think I’ve ever seen.
Just what do you think an axiom is? And how would you go about using one without logic?
The axioms and the axioms alone well define a mathematical space and avoid ambiguity and contradiction. Anything external to it has nothing to do with them and is, therefore, ill-defined, nonsense.
You’re avoiding the crucial question: what is an axiom?
To every other mathematician in the world, an axiom in a fundamental logical statement. A typical mathematical definition of an axiom is: “An axiom is a statement which is assumed to be true, and is used as a basis for developing a system. Any system of logic starts by saying clearly what axioms it uses.”
In mathematics, we start with a set of axioms that defines the formal system we’re going to work with in some logic – most frequently, first order predicate logic. Then we produce proofs by doing inferences within that logic starting from the axioms.
If you’re insisting that mathematical logic has no place in your mathematical world, then what is an axiom? And if you’re not allowed to use mathematical logic, how can you prove anything using an axiom?
An axiom is simply a premise. Didn’t you know that? Again, you are distorting my messages. The logic or rules of inference I use are well defined by the axioms of the the given math system. EEE
Reply to Doug: numbers in dfferent bases are different objects and cannot be equal. As far as I know, the natural numbers are defined by Peano’s postulates. If your natural number system is defferent state your axioms here.
This is consistent Mark, you keep misquoting me and making claims you cannot support. Point to at least one problem with my number system. When you refer to system of fractions you must specify the axioms of that system; othherwise, your statement is nonsense. Very sloppy, Mark. Brush up on foundations, at least.
Cheers,
EEE
Reply to MarkCC
I think your problem is blurred vision or confusion or lack of understanding of basic mathematics. You have repeatedly asked the same questions that I have already answered. EEE
So you would argue that 2 in base-10 and 10 in base-2 aren’t equal?
ES
reply to Thomas
Only the insecured are scared. Not just somebody but many reviewers and renowned peer reviewed jounals published my work. EEE
Reply to Thomas
What you don’t know scares you. You will not know those journals unless you publish there. EEE
Reply to Mechanical
Mathematics (and also science) is not a matter of belief or even intuition because a single error can be disastrous, e.g., the disastrous final flight of the Columbia Space Shuttle which was due to inadequate mathematics and guiding physical theory. Note that 1 and 0.999… are distinct objects and to say that 1 = 0.999… is akin to saying apple = orange.
With his claims that 0.999… and 1 are different objects, and that 1/3 expressed in base 3 (0.1) is a different object than 1/3 expressed in base 10 (0.333…), I have to wonder if Mr. Escultura even understands the distinction between an object and its representation.
This disconnect that you make, between the object and the representation, seems to be a common one in crankland.
I am thinking of cantor cranks here previously (name escapes me), who seem to have similar problems.
They confuse the map with the territory.
Reply to Peter,
The territory and its map are distinct; therefore, you cannot argue anything about the territory based on the properties of the map. EEE
Reply to MarkCC
You have a very superficial grasp of mathematics and rather mechanical and uncritical in your thinking. You cannot see the error in your definition. Anyway, an axiom is simply a premise and you cannot put a false premise and assume it to be true. Otherwise, you will have inconsistent premises or axioms.
Reply to Deen
In mathematics the symbols or mathematical objects are the REPRESENTATION OF THE CONCEPTS OF INDIVIDUAL THOUGHT. Such objects or representation are the subject matter of mathematics, not the concepts of one’s thought as explain elsewhere here.
Cheers,
E. E. Escultura
What are your axioms, then?
You’ve spent a lot of time claiming that the usual axioms of the real number system are flawed. You also say that your better system uses only three simple axioms.
Fine. I can’t find them. I realize google is far from perfect. Therefore, I’m going to the source.
What are the axioms of your system?
Not “what is the paper title?” Show us your axioms. If they are few and simple, you don’t need a whole paper to state them.
To demonstrate their value, yes. But to say what they are, no. Not if they really are simple.
Reply to Vicky
You have to find them in the sources I cited here or in my posts in other websites, e.g., False Proofs. EEE
Can you provide a website address?
Surely you’d like this groundbreaking work distributed?
ES
I have answered this question umpteen times. I think the problem stems from lack of grasp of axiomatic systems and Hilbert’s rectification of mathematics. EEE
For the nth time, if you want us to accept your axioms, you should be willing and able to state them. If it’s not convenient to put them here, give us a link to somewhere we can find them online. (Yes, I googled a bit, using your name.)
Otherwise, you’re saying “I’ve proven very important things, and I won’t show you the most basic things you need to understand the proof.” For example, you assert that your axioms enable you to prove that 0.9999999…. does not equal 1 is interesting. Without the axioms, there cannot be a proof.
As far as I can figure out, one of his axioms is “There is a one-to-one relationship between the base-10 representation of a new real number and the new real number itself.”
If you accept his axiom, then sure, 0.99999…. != 1.
But a whole lot of other things stop working. Near as I can tell, he basically just assumes that things work, because he says so. He never responds to problems – like the fact that if d* exists, then it’s necessarily a second additive identity.
Wrong again, MarkCC. EEE
Why is he wrong?! Prove him wrong, don’t just state things!
ES
If you can’t even see the difference between the object 1 and the object 0.99… you are hopeless. You have not understood Hilbert’s contribution. I think you and mark have the most serious problem with mathematics here. EEE
The objects are the subject matter of the math system I deal with. Their representation consists of different objects which are the subject matter of a different math system. EEE
Reply to Deen
What you need is a magnifying glass to distinguish the difference between the objects o.999… and 1. Or, maybe, you have not understood the discussions. EEE
Reply to Deen
In a mathematical system you deal with objects and define them by a set of axioms. If you represent or replace them by another set of symbols then you must well define them by another set of axioms to build another mathematical system. EEE
Reply to E. S.
To the extent that “2 in base-10” and “10 in base-2” are different objects,
they are different objects.
Reply to Deen
A system of objects is different from a system of their representations which are different objects. Each one can be built into a mathematical system with suitable set of axioms but they are distinct mathematical systems even if they are isomorphic.
You are all confused, Deen. You cannot even see the difference between 1 and 0.99… The subject matter of a mathematical space consists of objects regardless of whether they represent something else or not and, yes. the those objects and their representation are distinct.
I am no one to guide this thread, but I do believe we need some cleaning. At least I can not easily track all open issues.
Let prune the tree. If it seems right, continue from here. If not, please, ignore me.
To sum up:
First, we have here our host Mark, who I believe is the only one who remember the original question 🙂 : why are real numbers ill defined? What contradiction can be derived from its definition? This is still open.
Second. We have 0.99999… defined as the limit as n tends to infinity of the sum from 1 to n of 9 * 10^(-i). This is, 0.9999 is this limit, a way to write it. Why can not we say this limit is equal to 1? What commonly accepted axiom is in conflict with this? We could write this limit strictly, proving that it exists and all that. Will that settle the question?
Third. Mr. Escultura made a very controversial statement, that I believe practically destroys all current mathematics. “Any proof involving mapping from one mathematical space to another is flawed”. We can not even say if something is true or false, because we can not use a map from the statement to the space {true, false}. Why is this so?
Four. Mark ask what is an axiom for Mr. Escultura, or how can someone prove anything using just axioms without using mathematical logic.
I believe this summarizes the main open questions. Of course, if I forgot or misinterpreted something, my fault, so please fix it.
Sounds about right to me. I’m not holding my breath for answers, though.
The real numbet system is ill defined because its field axioms are inconsistent. The question of inconsistency of the field axioms has been answered many times.
You are again introducing an even more ambiguous term, limit. What is it? I’m sure your proof of existence of limit uses the axiom of choice which is false on infinite set.
Yes, the implications of some of my statements destroy current mathematics. But I do not just destroy anything. I replace it by something better. In the case of the real number system I replaced it by the new real number system.
Mathematical logic is external to a mathematical system and has nothing to do with its axioms. In other words, this rectification of mathematics that I have unddertaken makes mathematical logic irrelevant to mathematics. It may be relevant to ordinary ordinary reasoning. Even set theory is irrelevant.
Cheers,
E. E. Escultura
The axioms are simply premises and they must be consistent. An axiom cannot be false like the trichotomy axiom is (by virtue of the counterexamples to it) for it makes the set of axioms of the given mathematical system inconsistent. Conclusions in an axiomatic system MUST FOLLOW FROM THE AXIOMS. That is the only valid logic. External logic is not valid because it has nothing to do with the axioms. Mathematics can be destroyed only if there is no superior replacement. EEE
An axiom is a logical proposition and your argument is completely meaningless.
> Conclusions in an axiomatic system MUST FOLLOW FROM THE AXIOMS
How does anything “follow from the axioms” without using rules of logical inference?
You are thinking the old way. It does not help you in mathematics where tremendous changes have occurred. EEE
Well at least I’m thinking.
You are using the language of mathematical logic which which is ezxternal to and has nothing to do with an axiomatic system well defined only by its axioms. I think you suffer from old thinking which has been left behind by advances in mathematics. EEE
Please supply a proof that
1 != 0.999…
from your three axioms, without using any logical inference.
Who dictated the rules of inference, Andy? Mathematics is not a system of commandments or doctrines. It is based on rational thought. The axioms of a mathematical system are chosen on the basis of what one wants to do with it the only requirement being consistency. I constructed the new real number system not only for purposes of my mathematical pursuits but also as the core mathematics for the development of the grand unified theory in physics.
Reply to John
Introducing “limit” brings us to another ball game. I am only dealing with the mathematical objects 0.99…, etc. and building a mathematical system with them.
My statements are controversial and contradict conventional mathematics. Trying to resolve the controversy is the only rationale for this discussion.
The premises or axioms are the basis of of mathematical reasoning within that mathematical system. Mathematical logic has nothing to do with it; therefore, you cannot invoke it to make your mathematical arguments. EEE
Reply to John
1) One of the axioms of the real number system, the trichotomy axiom, is false, which makes the real number system nonsense and needs an overhaul which I did.
2) The sum is different from the limit; they are different objects.
3) You must examine first if the statement “Any proof involving mapping from one mathematical space to another is flawed” is true. If so, then the statement “it destroys all mathematics involving mapping from one mathematical space to another” is true.
4) I have been able to build a mathematical system without using mathematical logic at all.
Both MarkCC and John have missed the boat. I have answered every question raised here. Now state a question that I have not answered and I’ll answer itpromptly.
“x = 0.999…
10x = 9.999…
10x – x = 9
9x = 9
x = 1
Or…
0.9 = 1 – (0.1^1)
0.99 = 1 – (0.1^2)
…
0.999… = 1 – (0.1^inf)
0.1^inf = 0
0.999… = 1”
I’ll coment on this “proof” before I refer the viewers to the comprehensive dialogue on on Larry Freeman’s False Proofs” or the paper, Escultura, E. E. The new real number system and discrete computation and calculus, J. Neural, Parallel and Scientific Computations, 2009, 17, pp. 59 – 84 for the full discussion of these issues.
First of all, you cannot multipy a nonterminating decimal because it is ambiguous and this is true of any nonterminating (in fact, this follows from the ambiguity of infinite set). You can only approximate the product to desired accuracy.
Here, writing 10(0.99…) = 9.99… is not justified by any of the the field axioms.
Similarly, you cannot cannot add or subtract nonterminating decimals since this operation needs the last digits of the numbers to even start. Try adding sqrt2 and sqrt3 and write the result. Thus, the equation,
10x – x = 9
is nonsense and the rest of your “proof”collapses.
You are not alone; I had been teaching my students this erroneous proof for years.
Cheers,
E. E. Esccultura
For someone who repeatedly cites his own expertise as a mathematician, you’re amazingly ignorant of how mathematicians work with proofs.
You can just blindly assert things without justification.
You’ve redefined the entire concept of numbers in a completely non-sensical way, without justification.
You assert that the field axioms are inconsistent. But you ignore repeated attempts to ask you why? You can’t just say that they’re inconsistent and expect everyone to nod their heads and discard these fundamental axioms.
You assert that you can’t use logic to talk about math – which pretty much makes the entire concept of proof meaningless. But you don’t make any attempt to justify it.
You just assert that there is a one-to-one correspondence between numbers and terminating representations in base-10. But you ignore the fact that math doesn’t work if you do that.
You assert that numbers with non-terminating representations are ill-defined. But you refuse to justify that.
That’s not how mathematicians work. Mathematicians don’t make statements without justification. Mathematicians show proofs.
If you want to claim that the field axioms are inconsistent, you can do that. But if you’re a mathematician, you’ll show a proof of their inconsistency.
If you want to claim that there’s a one-to-one correspondence between real numbers and terminating decimal representations, then you need to prove that. And you can’t. Because to mathematicians, the field axioms are part of what defines the real numbers, and your version of the real numbers can’t satisfy the field axioms. In your definition of the real numbers, you can’t divide by three – because by the field axioms, division is multiplication by the multiplicative inverse; and the multiplicative inverse of three doesn’t exist in your system.
What you’re doing simply is not math.
I have answered every question here or if the answer is too long I refer the viewer to the original source. I HAVE NEVER ASSERTED ANYTHING ANYWHERE AT ANYTIME THAT I HAVE NOT ESTABLISHED.
Cheers,
EEEscultura
You have asserted all sorts of things here and have refused to show a mathematical proof of any kind, only words. If you truly wanted us to understand and believe your new system, you’d actually take the time to explain. Right now, what you’re doing is pretty much trolling.
Oh, and another thing… I’m not invested enough in your theories to purchase the ‘original sources’ (read: your books). Thus, referencing books that nobody here has is only likely to be seen as totally evading the question. You have to prove yourself before you can get us to buy the ‘original sources’.
You’ve also ignored several basic questions and tried to hide it by answering the questions you do answer (I’m still waiting on the proof that shows that 1 and 0.999… are different) in a location very separate to the original question. Yes, there’s a flaw in this comments section where you can’t just keep replying to a string of messages (a flaw of necessity, I believe, since you’d soon have VERY cramped messages), but you do this even when you are able to reply directly to a message.
Then you wonder why your apparently amazing new system is being rejected off-hand by the rest of us. Doesn’t really matter if it’s the next big thing, if you can’t explain it and use it, we’re going to keep criticising it.
Reply to both MarkCC and Mechanical
For the benefit of those who need repeated statements to understand them, I give the sources of Brouwer’s and my conterexamples to the trichotomy axiom:
Brouwer: his article in Bennacerat and Putnam, Philosophy of Mathematics, Cambridge University Press, 1985 and my article: The new real number system and discrete computation and calculus, Neural, Parallel and Scientific Computations, Dynamic Publishers, 2009.
MarkCC does not know how mathematicians work because he is not a mathematician.
All the axioms of the real number system are what I call the field axioms and they are inconsistent.
It is sufficient to refer you to published sources where I constructed the proofs of ALL my assertions here.
EEE
I’d ask how LEJ Brouwer published a paper with no collaboration 19 years after his death, but you’d probably ignore my question…
ES
You’ve apparently proven something somewhere about the trichotomy axiom (although even that is questioned by many). But nothing about the inconsistency of the 7 axioms listed above.
Reeply to Michael
There is no contradiction in the 7 axioms listed above but they don’t constitute the field axioms. EEE
I’m surprised that until now Mark has not understood my replies to all the questions. I cited where the counterexamples to the trichotomy axioms can be found because they cannot be reproduced here. I never make a claim that I cannot support. If you think otherwise, cite an instance.
Almost every paragraph here reveals misunderstanding of my posts and superficial understanding of mathematics. NONTERMINATING DECIMALS ARE ILL DEFINED IN THE REAL NUMBER SYSTEM. THE NONTERMINATING DECIMALS IN THE NEW REAL NUMBER SYSTEM ARE WELL DEFINED BY ITS AXIOMS.
> NONTERMINATING DECIMALS ARE ILL DEFINED IN THE REAL NUMBER SYSTEM.
No they’re not. See? I can just blindly assert things too.
Have you accepted the basic fact that the axiom of trichotomy is NOT one of the field axioms yet?
You can blindly assert things only when you don’t know what you are doing.
You are splitting the so called field axioms from the order axioms, etc. I don’t. I put all of them as the axioms of the real number system. You used all of them to build the real number system and called complete ordered field which is nonse.
But I know where you guys have problems. You do not know how to used citations (the mark of a nonmathematician). I have cited a source of my counterexamples to the trichotomy axiom and FLT. I cannot reproduce them here for obvious reason.
Wiles, Andrew (1995). “Modular elliptic curves and Fermat’s Last Theorem” . Annals of Mathematics. ISSN 0003486X.
Hey, look here! A citation! Wow, so I have the “mark of a mathematician”, again!
This is one (very complex) example on why are you wrong. There are more easily understood ones. Look, another reference:
Jacobs, Harold R., 1979. “Elementary Algebra”. W. H. Freeman.
If you find it too difficult, try this one:
Clemens, Meg, 2003. “The Every Kid’s Math Puzzles Book”. Adams Media.
You are talking about proofs in conventional, unupdated mathematics. That is what your problem has been. That is why you are unable to contribute to mathematics which could have improved your understanding of mathematics. EEE
Reply to MarkCC
I grasp mathematics firmly because I do it every day and I have contributed to it immensely (an understatement). EEE
Reply to MarkCC
How do you know how mathematicians work when you are not a mathematician?
I have never made any claim that I did not justify. If you cannot understand my work, that is your problem.
How do you know how mathematicians work, MarkCC, when you are not a mathematician? What you know is based on hearsay.
0.999… = sum k=1 to N of 9/(10^k) with N->inf (by definition of the “…” notation)
10*0.999…. = 10*sum from k=1 to N of 9/(10^k) with N->inf
= sum from k=1 to N of 10*9/(10^k) with N->inf (by distributivity)
= 10*9/10 + sum from k=2 to N 10*9/(10^k) with N->inf
= 9 + sum k’=1 to N from k’=1 to N’ 9/(10^k’) with N’->inf (k’ = k-1, N’ = N-1) = 9 + 0.999…
Where’s the contradiction with the field axioms?
You cannot find a contradiction when you obfuscate the issue by putting in even more ambiguous concepts such as limit, infinite sum, etc. What are they anyway? EEE
Oh, at least you are ready to learn (at least, you are asking what you don’t know).
“Obviously I can not write here” what a limit, infinite sum and other elemental concepts are, but… a citation!
Study this:
Weiestrass, Karl, 1854. “Zur Theorie der Abelschen Funktionen”.
If you are referring to limit in the sense of calculus, it is ill-defined, nonsense. I well define limit in my mathematics. You have to read my original work and find a flaw in it. EEE
Oh, at least you are ready to learn (at least, you are asking what you don’t know).
“Obviously I can not write here” what a limit, infinite sum and other elemental concepts are, but… a citation!
Study this:
Weiestrass, Karl, 1854. “Zur Theorie der Abelschen Funktionen”.
I create my own mathematicsfor my purposes based on my critique of conventional mathematics which is self-contained. Therefore, I do not need the work of others. What you need to do is find a flaw in my work. So far none of the experts (published mathematicians) found any. EEE
Reply to Deen
You cannot see the contradiction in nonsense; all operations in an ill defined number system are nonsense. EEE
Well done! Of the three proofs suggested here, you’ve managed to ‘disprove’ exactly one. One of three ain’t bad, that’s 33.333…% Oh wait, we can’t write that… My bad.
Of course, you took the standard ‘nuh-uuuuh’ approach. And, of course, there’s a flaw in your approach also.
When writing 0.999… We have represented ALL the decimal places. There’s an infinite number of them and we’ve just written them.
When writing sqrt(2), we write 1.41421 and I think I can safely say that’s about as far as most can get off the top of their head. And even if you could go to a thousand decimal places, yes, you’re right, you can add it *exactly* to any other number. That’s why in maths, if we want an exact number for [sqrt(2) + sqrt(3)], we can’t simplify it.
In summary, sqrt(2) can’t be fully represented in decimal form, 0.999… is already fully represented in decimal form. Thus, we can use 0.999… as we wish, without losing any accuracy, because it’s exact.
Finally, even if we agreed that that proof was flawed, disproving one proof doesn’t necessarily mean you’re right. It’s a typical failed tactic which I’m disappointed to say I fell for. You have to prove it, as I said in a previous post (in which you responded to the earlier part, but amazingly missed this part):
‘Now prove that they’re different. Don’t hide behind fancy words or simply state things that you haven’t proven, or bring random other theorems or concepts into the mix seemingly out of nowhere only to dismiss them, or (as I let you do already, d’oh!) attempt to disprove other proofs, algebraically prove it. If your system is worth anything, you should be able to use it, instead of words, to prove how we’re wrong and show that this system of yours is consistent, useful and functional.’
1 and 0.99… are different because THEY ARE DIFFERENT OBJECTS. Period. Do you see the difference? EEE
‘If your system is worth anything, you should be able to use it, instead of words, to prove how we’re wrong and show that this system of yours is consistent, useful and functional.’
How many times do I have to say it?
Reply to Mechanicall
The new real number system is the main mathematics of the grand unified theory (Escultura, E. E. The mathematics of the grand unified theory, keynote address at the 5th World Congress of Nonlinear Analysts, published in J. Nonlinear Analysis, A-Series: Theory: Method and Applications, 2009, 71, pp. e420 – e431). EEE
He doesn’t listen, does he?
Reply to Mechanical
1) FYI a single error collapses a mathematical system.
2) State a flaw in my approach.
3) I understand this notation: 0.999…;
4) 1.41421 is not the same as 1.41421… and former is only an approximation of the latter; they are distinct.
5) You can’t write or find the sum of sqrt(2) and sqrt(3) because in adding numbers you need their last digitswhich they don’t have. This is due to the fact that a nonterminating decimal is ill-defined.
6) You can represent any number, if it exist, by any appropriate symbol. What you can’t do is find the sum sqrt(2) and sqrt(3) because it does not exist.
7) I cannot prove the existence of something that does not exist.
8) It is enough to exhibit your errors. I never use fancy words or nonsense unless you are seeing things. What a confused mind.
It’s sloppy to write sqrt2 = 1.41421 because a nonterminating decimal is NEVER equal to a terminating decimal.Moroever, there is ambiguity in 0.99… because you cannot ccompute with it. For instance what is
5(0.99…)? Please write thes product. EEE
Try rereading my post, E, I specifically said that 1.141421 doesn’t exactly equal sqrt(2). In fact, I even said that sqrt(2) can’t be fully represented in decimal form.
Also, 5, just like I’ve been saying. Care to actually show us why 0.999… doesn’t equal one by actually using maths, rather than talking about unrelated truisms and shouting ‘THEY ARE DIFFERENT OBJECTS!’ repeatedly?
*1.41421
Reply to Mechanical
That is exactly what I mean: You cannot write sqrt2 or
5(.99…), you can only APPROXIMATE it. I think your problem is language. EEE
Reply to Mechanical
1) I asked you to find the sum of sqrt(2) and sqrt(3) and you wrote other numbers. You seem to have difficulty with the English language.
2) 0.999… isn’t even well defined; how can I compare it with 1? Can’t you distinguish different objects? Check your eyes?
I cannot handle all the nonsense here and I have pointed out too many.
> you cannot multipy a nonterminating decimal because it is ambiguous and this
> is true of any nonterminating (in fact, this follows from the ambiguity of
> infinite set). You can only approximate the product to desired accuracy.
5 * 1/7 = 5/7 = 0.[7142857]…
Where is the approximation here pls?
If you won’t let me do this, then how about I translate it into base-7:
5 * 0.1 = 0.5 (allowed)
Then translating back into base-10 I get 0.[7142857]…
Try adding sqrt2 and sqrt3 and write the PRECISE answer here. EEE
Way to TOTALLY avoid the question asked of you. You’re confusing repeating and non-repeating decimals (and yet you claim pi and e are precise)
Maybe you could type the PRECISE value of pi here?
There is an algorithm for computing pi or e but you cannot write either precisely as decimal. That is part of the inherent ambiguity of any nonterminating decimal. In my new real number system I can only contain such ambiguity by approximating it by a terminating decimal within desired error. EEE
As pointed out above, there’s an algorithm for calculating the decimal expansion of 1/3 too, and it’s hell of a lot simpler than the one to calculate pi.
Your objection to the reals does not stand up to even the most cursory of examinations.
Reply to Any
1) Only fractions whose denominators do not have prime factors other that 2 or 5 are well-defined. What you wrote on the right side of the equation is ill-defined, does not exist.
2) Base 7 belongs to another number system. A mapping does not help your case
What are those dots? Unless you tell me EXACTLY what those dots are what you have written are ambiguous.
What are those ellipses (dots), Andy? They are the errors.
Correction. The expression above should be:
10x – x = 0.99… is nonsense. EEE
“How do you explain that EACH BASE SYSTEM has a different set of natural numbers?”
This question is vague. If you mean by natural number the integral part of a decimal in a given base, naturally, they differ from one base system to another because they belong to different mathematical systems.
Cheers,
E. E. lEsc ultura
Yet if I have 12 marbles in my hand, the number “12” in the decimal system refers to exactly the same number of real-world objects as “1100” in binary, or “14” in octal, or “C” in hexidecimal. You claim those are all different numbers, but aren’t they just different representations of the same number?
Looks like E.E.’s position comes as refutable by anyone who just knows the concept of a natural number and knows that natural numbers can get notated in different ways… no need to know anything about rational or real numbers. A caveman could probably do it. I mean, according to him, when the Babylonians used a base 60 system, they used different natural numbers than we did. Since the Mayans used a base 20 system, they used different natural numbers than we did. The dozenal soceity http://everything2.com/title/Dozenal+Society+of+America is promoting using different natural numbers than we use, according to E. E. Escultura. It would come as one thing if someone could claim I had exaggerated his position, or I had interpreted what he said. But, he’s implied *exactly* this.
You are referring to correspondences. Math systems in 1 – 1 correspondence need not be the the same. Certainly, the system of integers are NOT THE SAME AS the system of binaries.
Cheers,
E. E. Escultura
You again missed the distinction between the concepts of thought and their representation by objects in the real world like symbols. Only the latter can be studied mathematically. Different objects like 1 and 0.99… are never equal.
That’s your assertion, but you haven’t actually proved it.
In your system, can you define the multiplicative inverse of a number?
Can you define division? In real numbers, division is an operation (/) such that
, and 
.
How can you show that in your system?
In your system, 1 does not equal 1 and I will prove it thusly:
1 = 1
According to you, only one representation for the number one should exist. But i can see two distinct representations there: one to the left of the equals sign, and one to the right. Therefore, they are not equal and comparing them is nonsense like saying banana = kiwi.
Tell me the name of any mathematician who found a flaw in my work. I mean, real mathematician, i.e, published mathematicians, not a crank. EEE
Send me your work. I’d happily go out and find a published mathematician to prove a point. I’ve got free time…
Binary numbers are distinct from decimals even if there is some correspondence between them. EEE
Reply to Deen
What you can say correctly is: the decimal 12 is written 1100 in the binary system and they are different objects belonging to different number system.
A set of objects like marbles and their representations, which are also sets of objects, can be built into different mathematical systems with its own set of axioms which are distinct even if they may be isomorphic to each other. Mathematically, they are independent.
Is “1” in base-2 the same number as “1” in base-10?
Or better, still.
We have 1234 in base 10. But wait, no, we can reinterpret it.
Suppose we don’t interpret it as 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0. No. We will interpret it as a number in base 100. Now, instead of the then symbols 0, 1, .. we will have a hundred symbols 0, 1, 2, .., 9, 10, 11, 12, .., 99. This are now digits in our system of base 100. We use 15 as we could we F. Then our number is
12 * 100^1 + 34 * 100^0.
But, of course, this is a different number, and can not be mixed with the previous one.
I know programmers group binary digits in groups of four, reading them as hexadecimal numbers. But, hey, they are now different numbers!
Depending on how you group the signals in the wires, you got one number or other! Cool!
I can imagine our friend in school:
– Teacher: “Today, we’ll learn Bolzano’s Theorem. Let f be a continuous function on the closed interval [a,b], with…”
– EEE: “In what base?”
– Teacher: “Eh?”
– EEE: “In what base is a?”
– Teacher: “Errr… in any base. In any. The theorem is independent on the representation of the numbers.”
– EEE: “But that can’t be. In what base is a?”
– Teacher: “It’s irrelevant. In any base.”
Or with a meter with two scales (centimeters and inches) with two scales, one with grams, and the other with pounds, measuring something.
– Person: “How long is that thing?”
– EEE: 25 inches.
– Person: “In centimeters?”
– EEE: “No, no, no, that’s a completely unrelated number. There is no useful relationship between the two.”
– Person: “But the object has a definite length!”
– EEE: “No, no, no. The object has a different length depending on the units you use. And you can not relate the two in a proof!”
The possibilities are endless.
Obviously, the “with two scales, one with grams, and the other with pounds” shouldn’t be there. I was writing the conversation about masses, and changed it to be about lengths, and that errouneously remains.
Thanks for the laugh. But, that’s actually consistent with E. E.’s position!
To John
Your name dropping is impressive but the calculus that you and I know is base 10. The dialogue you bring in is irrelevant. If you are trying to bring in some humor, its a bit corny. EEE
The calculus that most people know doesn’t have any “base” whatsoever.
Presumably though, it’s tricky to do algebra in the new real number system when equations as trivial as ‘y=x/3’ give a completely different set of solutions depending on the base.
So, the derivative of x to the second power equals two times x in base ten, but it equals *what exactly* in base 2? How do derivatives and integrals work in base 6, in base 8, in base 12? How do they work in base x, where x indicates any natural number? How does 10 in base two differ from 2 in base four? Perhaps you would do better to actually develop your “hypothesis” before parading it about as correct. And so what if you’ve “published” something here? The arguments speak for themselves, and no questionable appeals to authority ought to remain unchallenged. Try standing on the sole basis of your arguments Mr. Escultura.
Reply to John
1) In mathematics we dealing with real objects, symbols, etc., not interpretation.
2) A responsible blogger does not copy the errors of his teacher.
3) If you are a chemist, John, and you don’t distinguish between inch and centimeter your mixture will explode right under your nose.
NEVER. EEE
Reply to Mark. You have not grasped Hilbert’s contribution. The concepts of thought are ambiguous for reasons explained umpteen times. Only objects in the real world including representation of thought can be dealt with mathematically. All the concepts I have used here are well defined in the paper, Escultura, E. E. The new real number system and discrete computation and calculus, J. Neural, Parallel and Scientific Computations, 2009, 17, pp. 59 – 84. I can’t spoon feed them to you in a silver platter. EEE
No. EEE
No, Andy; they belong to different mathematical systems.
i’m far from being a mathematician, but my inner amateur linguist takes one look at the notion of “a decimal in a given base” and says, “you just gave the base; if it’s a decimal, the base must be ten.“
No. The natural numbers are defined by Peano’s postulates and the integral parts of the decimals are the integers. They are distinct but isomorphic. EEE
Yes, by definition. What is your point?
Reply to Nomen
You are right and I admire your lack of pretenion. EEE
What is your point, Nomen? Are you stating a definition by a linguist?
So, the number Z, expressed in base R
Z = a3 a2 a1 a0 . b0 b1 b2 b3
where ech a0, a1, … are digits, which by notation means exactly
Z = a3 * R^3 + a2 * R^2 + a1 * R^1 + a0 * R^0 + b0 * R^(-1) + b1 * R^(-2) + b2 * R^(-3)
is in a “different mathematical space” depending on the value of R.
Cool. The Romans’ mathematics were different from ours! If we count with points, truths can be different! If we decide to forget about the convenience of writing numbers in figures, math changes! (As we all know, every theorem references in what basis do they work).
And, what happen with numbers noted by limits? e, pi? Well, they are an ‘e’, not a sequence of digits. Other space! Not under the law of the same axioms!
So, by the same logic, if we express a vector V of a vector space S in a basis {i}, V = sum( v_k * i_k ), it is not the same vector if we change basis {j}, V = sum( v_k * j_k )!!!
And we can not relate then, and prove things independent of the basis.
Very useful and intuitive your “consistent axioms”. Are they been rapidly accepted? Good luck waiting Nobel price.
Jajajaja. This stopped being funny. It’s just ridiculous. Our friend is so focused on notation that he has forgotten math.
By the way. 0.9, 0.99, 0.999, 0.9999, … is the sum of geometric series. It’s limit is 1. This is exactly what one writes in the form 0.9999…. Notation, notation, notation. I refer you to any book, as rigurous as you want. Of course, I know, I know, “limits are wrongly defined” “Why?” “Because I say so”.
By the way 2. Willes & cia. (the math community) are peer reviewed, too. Of course, we may have a different idea of what “peer” means.
By the way 3: I tried, you can not denny we tried. We tried you to answer why are real numbers inconsistent.
Your problem, which applies to all of you here, is that you do not know how to use citations (the mark of a nonmathematician). I have referred all your questions to the original sources. Can’t spoon feed the mathematics toyou; they are impossible to reproduce them here for obvious reasons. EEE
Your problem is that your references are nonsense, too. You can not write a post, you can not write a paper.
Most of the papers you have cite to are the same as your posts: I proved, I did, I I I…. and where it is a “proof”, it is obviously flawed and based on erroneous assumptions. (Which is normal, is you try to proof without logic).
You want us both to “think critically” and to blindly accept you are right because elsewhere there are proofs for all your nonsense.
Well, bad luck, some of us read you’re referenced papers, and they are nonsense, too.
You don’t know mathematics and you don’t know to argue.
In any case, why are you insisting we (the commenters) are so dumb, when you know no mathematician takes you seriously?
I mean, you say we don’t think critically, we don’t know what a citation is because… because… well, because you say so, we don’t we don’t we don’t… And for the rest of people? And for the mathematicians? What is the excuse?
A piece of work is nonsense to one who does not understand it and that is not the problem of the author. EEE
If I were to publish a paper using an esoteric new notation I’d just invented that bore no resemblance to the usual, and people began to call my paper “nonsense”, when I could easily use their notation and produce the same results, I think that would be my problem.
Reply to John
Notation, definition and representation are equivalent and you can write them interchangeably PROVIDED the objects, symbols, etc., belong to THE SAME NUMBER SYSTEM. Otherwise, they are nonsens.
Roman numerals and decimals belong to different number systems.
You been asking me questions and my answers are right before your eyes. Have your eyes checked.
John has not grasped what we have been discussing here. All he needs to do is keep re-reading the posts. Useful advise: rely on yourself rather than on mathematicians of the past. Otherwise, you will not see their errors. Mathematics advances by rectifying its errors.
So there’s this thing called R*, which is R but with two new things called d* and u*.
The 9s of 0.999… trail off into the darkness, and somewhere in that darkness is the d*, so that 1-d*=0.999…
Also,
x+d*=x
xd*=x
x+u*=u*
xu*=u*
And hey now, “Numbers like u* − u*, d*/d* and u*/u* are still indeterminate but indeterminacy is avoided by computation with the g- or d-terms.” (Quoting paper from his website.) Because to avoid doing messy things in the dark, we just cut the tail off a non-terminating decimal.
Finally, the real numbers are saved! It’s so much more consistent now! And well-defined!
There is some sense in this post. Unfortunately, the last sentence is problematic because the inconsistency of the field axioms remains.
Cheers,
E. E. Escultura
Reply to bibliovore
FYI, d* and u* are not real numbers and it is nonsense to apply any binary operations to them.
No bibliovore, the real numbers have given way to the contradiction free new real number system.
I just spent some time looking into various online commentaries on Mr. Escultura’s work and personality. Discussing mathematical cranks is fine and amusing and everything, but is it really worth it to argue with someone like this when they are clearly not all there mentally?
(And I really don’t mean to insult Mr. Escultura by putting it that way.)
As I said the real cranks are those who do no know that they are doing or what they are talking about. You find most of them on this thread.
Anyway, as a final remark on this crankery, I think the most difficult thing to grasp is what Hilbert did a hundred years ago. It is a recurring weakness here and in most threads I have seen. I attribute it to lack of critical thinking. I think this is the main reason most of the bloggers here are unpublished. I would advise everyone to think really hard and grasp the significance of Hilbert’s contribution.
Cheers,
E. E. Escuiltura
Shorter E.E. Escultura: “I’m not crazy, everybody else is!”
Odd that a lot of Hilbert’s work uses real numbers… why’d he do that if he was so against them?
ES
No, ES, he partially fixed the foundations of the real number system because he saw its defects. He left others to complete it.
Pretending to know and exp0unding on mathematics without even looking at the original source and having nothing show that he is a mathematician(published), isn’t it the hallmark of a crank? EEE
No, Mister.
You’ve got your definition of a crank wrong. Buy a dictionary along with some math book (preferently one of Hilbert).
A crank is a person who defend theories which are evidently wrong or empty and nonsensical, and who believes have accomplished a lot of feats (like solving the n-body problem, proving false FLT, discovering the ToGU, inventing a source of free energy, …) with a few people showing them why they are wrong (people like Mark), and most people ignoring them.
And, despite most people ignore them, and they believe they invented things which would make them rich, they are not rich nor acknowledged nor anything, and in two years nobody will remember them.
To sum up, a crank is a guy who solved the incompatibilities between General Relativity and Quantum Mechanics but can not solve a simple math problem of an elementary book.
This definition remembers me of some guy…
Reply to John
Youe peoblem is you have no originality and depend on books and thinkers. EEE
No one could accuse you of having read any books, that’s for sure.
You are right, John, defending the real number system is a ticket to crankdom.
Why do cranks hide behind userame? Because they don’t want other cranks to have a full view of the ignorance partially revealed by their posts. EEE
I think you have to check your vision apricissimus. I have replied to all the questions asked online including those I have answered here. Point to one I haven’t.
Interesting that ee talks so much about Hilbert then flaunts that he is ‘published.’
>>”I attribute it to lack of critical thinking. I think this is the main reason most of the bloggers here are unpublished.”
To recap, MarkCC posted simple field axioms and asked ee to explain how they are inconsistent. In response, how I understand it, ee cited different axioms, which he didn’t even bother to write, and then stated that he had wrote a proof showing that they were inconsistent. Other conversations took place, but about Mark’s main topic I have two things:
First, suppose Mark had originally chosen to list whatever axioms ee referred to instead of the canonical ones he did write. Ee still didn’t give a proof that they were inconsistent.
Second, if ee’s proof just shows that the field axioms he uses are inconstant, then the canonical ones that Mark wrote are safe. So basically the axioms that one considers when talking about ‘field axioms’ are not what ee claimed to be inconsistent.
Yeah, why does he keep talking about the trichotomy axiom? There are 7 axioms listed above. None of them is the trichotomy axiom. And he has never proved that there is an inconsistency. I keep coming back every few days to check up, but still nothing from him except his assertion that he has indeed proved his point. That is so strange. It makes you really wonder what is going on in his head.
ee, please just lay out the proof starting with Mark’s 7 axioms. Should be easy to do if you already know there is an inconsistency.
Or is he really claiming that Mark is using the wrong axioms? I’ve never heard him say that either.
He keeps claiming that trichotomy is one of the field axioms, and even cites Royden (3rd ed, I’m guessing from his page numbers) as evidence. Unfortunately for Escultura, Royden, like everyone else, never says that trichotomy is one of the field axioms. The field axioms are listed in section A, beginning on page 31, while the order axioms are clearly distinguished and listed in a separate section B beginning on page 32.
The axioms of the real number system include the order and trichotomy axioms. I call all of them the field axioms for, together , they establish that the real number system as a complete ordered field which is nonsense. EEE
Then you use “field axioms” in a manner inconsistent with the rest of the mathematical world.
Additionally, the field and order axioms do not together define the reals as a complete, ordered field. The rational numbers, for example, also obey the field and order axioms, including trichotomy, yet are not a complete, ordered field.
I think the main problem here is blurred vision. Try again reading the posts from the top. Use a magnifying glass. You might find the answers to your questions. EEE
I combine the field, order and trichomy axioms in one set of axioms for the real number system for they supposedly establish the latter as complete ordered field which is nonse. EEE
I don’t flaunt anything. I state the facts. Publication is the mark of a mathematician. EEE
And the mark of a physicist; witness El Naschie.
Reply to mike
I’m not flaunting or bragging. I’m citing facts that can be verified, ALWAYS.
The field axioms I’m referring to are the field and order axioms in Royden’s Real Analysis, 1966. EEE
Reply to mike
I cannot reproduce here complicated proofs or counterexamples. You must read the original papers and if you cannot understand them that is YOUR problem, not mine.
Mike, the axioms of the real number system which I call field axioms are in Royden’s Real Analysis, pp. 31 – 32. You just keep re-reading the posts and you’ll see that I have responded to all questions raised here.
Neural, Parallel and Scientific Computations is certainly a great journal. According to MathSciNet, it even got two citations to some of the 97 items it published between 2004 and 2008.
Dr. Escultura certainly publishes in as good journals as that. His articles appear in the MathSciNet database, but “There will be no review of this item.”
I am curious about one of the articles, where Fermat’s theorem is “solved”. What did he “prove”? Was Fermat right, or wrong?
He provides counter-examples to FLT involving his “dark number” d* = 1 – 0.999…
Since it has been proved to him time and time again that his d* must necessarily be identical to zero he is of course doing nothing more than writing down the trivial case “x^n + 0^n = z^n” in terms of multiples of d*.
Even if you accept d* != 0 he himself says that d* is not even a real number let alone an integer, so what it’s got to do with FLT, no one knows.
Reply to quim
Peer reviewed updated journals ARE NEW and it takes years to digest them. Their articles there have passed rigorous reviews. I started publishing there in 1997. It is, of course, a pleasant surprise that several papers of mine have won some honors like being among the most download articles published by Elsevier Science. The journals they publish are among the top rate in impact factor. For example, Nonlinear Analysis, Series B: Real Wolrd Problems ranks 2nd. BTW, one of my papers, was the basis of my nomination for the Nobel Prize for Physics in 2005, see:
http://bmhegde.com/hegde/articles.php?article_id=198
I think this post reflects ignorance and sourgraping.
Here is aniother example of ambiguity and sloppiness. I did not solve FLT; I proved it false by counterexamples. In otherwords, Fermat’s conjecture is wrong. EEE
Ambiguity and sloppiness all yours. The title of the paper is “Exact solution of Fermat’s equation (a definitive resolution of Fermat’s last theorem)”
Why do cranks hide behind their usernames? They want to keep other cranks from having a full view of their ignorance partiallyrevealed by their posts. EEE
What is ambiguous and sloppy about that? Or, do you even understand what you are saying? EEE
You write a paper titled “Exact solution of Fermat’s equation…” and then you write “I did not solve FLT; I proved it false”. You accuse me of being “ambiguous” and “sloppy” for what?
Reply to quim
This is all confused: Let me repeat for the umpteenth time what I have said. The real number system is nonsense since its axioms are inconsistent. Therefore, FLT being formulated in it is nonsense and cannot be resolved. Therefore, I have rectified the real number system by reconstructing it into the contradiction free new real number system, reformulated FLT there and resolved it. The resolution: FLT is false.
I proved FLT is a false conjecture by Fermat. EEE
Reply to quim. If you cannot even see that the solution of Fermat’s equation is a counterexample to FLT you are hopless. EEE
So you “resolved” FLT, but you did not “solve” it, because what you “solved” was the equation? Not only you rewrite math… you should rewrite the dictionaries!
Just in case you did not notice (you are somewhat slow). 1) You claim to have a counterexample to FLT, but you don’t show it. 2) You claim you don’t have a counterexample becuase FLT is ill-defined (should be ill-posed, but…) 3) You claim I am ambiguous and sloppy, but don’t say where. 4) You claim I cannot see that the solution of Fermat’s equation is a counterexample to it, but what I cannot see is that damned solution. 5) To solve does mean “To find an answer or solution to a problem or question” and is often used for conjectures. 6) I happen to be a professional mathematician. I made a mistake by writing to you. I won’t make a second mistake by telling you my email account.
Check your vision, quim. I never said I solved FLT. I resolved and found it to be false.
You cannot even read straight English. I did not prove FLT. I proved it false. EEE
Reply to quim
NPSC (published by Dynamic Publishers) is one of the renowned new updated peer reviewed scientific journals and it takes time for new ideas to sink in and be cited, especiaally, when they are revolutionary like my work is. EEE
I have proven Fermat’s conjecture, popularly known as Fermat’s last theorem, false, quim. All the journals I publish in – over a dozen of them – are peer reviewed. There is not even a single refutation of any of my papers there.
What a disappointing result. There will be no proof coming, will there? Or not even an attempt at a proof?
I was hoping so, but apparently not… Seems Escultura is running back to his journals, which don’t argue back
You will surely become famous if you can prove something that has been proved to be false. EEE
Mr. Escultura,
I think what people are asking for is a counterexample to show that the field axioms are inconsistent. And you have not provided one.
I think your problem is blurred vision. Read the posts here from top to bottom and you’ll find one repeated many times. If you can’t use a magnifying glass. EEE
I combinethe 7 axioms listed by Mark and the order and trichotomy axioms for they supposedly establish the real number systems as complete ordered field which is nonsense.
You cannot even understand what my posts have been saying. I have cited several times the original source of the counterexamples to FLT. EEE
I cited the original source for my counterexample, apricissimus. It’s not simplistic and I can’t reproduce it here fully.
Not likely.
You “proved” “something” “false” which Willes previously proved to be true. For some unknown meaning of “proved”, “something” and “false”.
Yet no mathematician acknowledges your existente. You are far from fame.
(By the way, it’s very funny you try to convince us by authority, when no mathematician takes you seriously).
Publication of work in peer reviewed scientific journal is an acknowledgement. Most of all, it is the responsibility of a mathematician or scientist to point out an error if it exists and refute whatever is erroneous. Otherwise, published scientific work stands. That is the way it is and no amount of sourgraping can turn the scientific world upside down. EEE
I believe you understand nothing.
No, Mr. Escultura. Something is not true because you publish it and nobody bothers to refute it. People have better things to do (except for us in this forum).
“What someone says is true unless some other person took the work to refute it”. Hahahaha, it’s the dumbest thing I’ve heard. You seem to have the maturity of a child, believing the center of the Universe.
In any case, every (EVERY, think of it) mathematical publication refutes you, so even with your argument you can not win.
Do you really believe any mathematician takes your “ideas” seriously?
Your problem is you never understood Wiles “proof” nor my counterexamples because you don’t publish and yet you pretend to know and expound on mathematics. Is that not what a crank is? EEE
And who can “pretend to know mathematics”? Cite anyone published. Willes? Hilbert? Cite one not in flagrant contradiction with you.
As I said previously, you should not use authority arguments when you have all authorities against you. No, bad idea.
By the way, I hallucinate with your bad logic. If a person who has not published “pretends” to know mathematics, then he is a crank.
Very very good logic.
I will help you.
When you publish, you let other people to judge your work. Publishing does not make what you say true, it makes it public. That’s why they call it “publish”.
In your case, you published in that very notorious journal (ahem), and then your ideas were public. And what happened? People judge them. Mathematicians judge them (probably very fast).
What is the result of all that? They though your ideas were nonsense, so anyone took them.
Studying current mathematic literature we can say nobody takes your ideas seriously, so now we know you know no mathematics.
And what with people who has not published? Well, the most probable thing is that they know no mathematics… beyond current knowledge. Yes, my friend, you can not publish and still study what others have published. Because it is public.
It doesn’t take an Einstein to see this. Not only you can not reason about mathematics. You can not reason about mathematics, you can not reason even about elementary subjects!
Publication of a piece of work is acceptance by the reviewers and you have been claiming that no one accepts my work. This is simple nonsense. Can you give a name of mathematician (published) who rejects my work? EEE
I think you are seeing things, John. You need to see a specialist.
No proof will ever come to a false conjecture, Michael.
Now, I know. Non-mathematicians do not know how to use citations. I have cited a source where I constructed the counterexamples to the trichotomy axiom and FLT. They cannot be reproduced here for obvious reason. What do you call a nonmathematician who pretends to know and expounds on mathematics? Crank, isn’t it? EEE
No, Mister.
First, your papers are nonsense. Yes, you put a citation. We read them. They are nonsense, like your posts.
Second. You’ve got your definition of a crank wrong. Buy a dictionary along with some math book (preferently one of Hilbert).
A crank is a person who defend theories which are evidently wrong or empty and nonsensical, and who believes have accomplished a lot of feats (like solving the n-body problem, proving false FLT, discovering the ToGU, inventing a source of free energy, …) with a few people showing them why they are wrong (people like Mark), and most people ignoring them.
And, despite most people ignore them, and they believe they invented things which would make them rich, they are not rich nor acknowledged nor anything, and in two years nobody will remember them.
To sum up, a crank is a guy who solved the incompatibilities between General Relativity and Quantum Mechanics but can not solve a simple math problem of an elementary book.
This definition remembers me of some guy…
Naturally, what you can’t understand you call nonsense. And now you bring relativity and quantum mechanics. Do you understand them? If you think a theory is wrong it is your responsibility to refute it. Where is it? And even if you can do it will not make it to the foot note of history because it is transparent to the official arbiter of scientific merit – the network of peer reviewed publications. EEE
It’s not me the one who call your work nonsense. Take a look at serious mathematical publications. If you find a trace of your ideas I will shut up.
I see you don’t understand how peer review works. Yes, you have been under the scrutiny of peer review, and sorry, you lost.
Peer review is not in getting published, it is in getting your ideas accepted. You publish something, and if it has value and is not bullshit others will take your ideas and develop theirs based on yours.
That’s how science works. That’s how knowledge advances.
Look at it. Your ideas are ignored. Nobody acknowledges you. Not me. Anybody. ANYBODY. ANY MATHEMATICIAN. Peer review works flawlessly. Sorry for you and your prepotency.
The first requirement of a mathematician is: he has contributed something to mathematics, i.e., he has some publication in peer reviewed mathematical journals. Short of this, he can’t understand current mathematics. In other words, a mathematician learns by publishing not by reading books. When something is published it stands unless refuted and it is the responsibility of a mathematician to point out error and refute the publication.
It is a contradiction to say that a published paper in PEER REVIEWED journal is ignored.
When a paper is published it means that the reviewers accepted the paper and all the ideas in it. Otherwise, it gets rejected.
That is how mathematics and science advance. When a paper is quite advanced, especially, when it is revolutionary, it takes time to become a material force for research although some of my papers have been cited by researchers. The new real number system paper, in particular, has been cited several times.
I know how peer review works. I have been there over 50 times and I passed. Have you?
I agree, you have not ackowledged any of my paper. All indications tell me that you are not a reviewer.
Cheers,
EEE
Cite them, cite the research papers citing your “new real number system”. We’ll be very interested in see how they use them.
Is it to ask for too much?
> “it takes time to become a material force for research”
Usually not for this kind of revolution. The n-body problem! The Grand Unified theory! A new real numbers! Sqrt(-1) is wrong! Come on, Willes’ proof was cited almost immediately!
We are speaking of articles dating from 1997 to 2005. 14 to 6 years old. If you’re still waiting for acknowledgement, well, don’t wait standing.
Say an amount of time. Five years from now? Ten years? I’ll be very glad to continue this conversation in ten years. That way we’ll see if someone remembers you, or if the imaginary number and reals and limits are still with us.
There are too many wrong theories for any one of us to refute them all. However, I put your own challenge to you: give us the integers x, y, z, and n that refute Fermat’s last theorem.
And, once again, I have no idea if I could understand your axioms, because you will not show them to me. If your axioms are too long to fit in a comment here, put them on the public Web. Link to them. Simple HTML or PDF or TeX.
Why do you hide this revolutionary system from the world? Web space is available all over the place.
I can give you a free Dreamwidth invite code, if you need someplace to blog that won’t try to grab your intellectual property rights. Just post your email address and I’ll send it.
You have missed many posts that respond to your quesstions. Or, you don’t know how to use citations. EEE
Reply to John
Can you name a mathematician who cites Wiles NOW, 2011? EEE
I don’t pretend to fed the troll anymore (I’m tired of it), but for the rest of people this comment gives the opportunity to show some (complex) mathematics related to Wiles’ proof, in case anyone is interested:
C. Breuil, B. Conrad, F. Diamond, R. Taylor : On the modularity of elliptic curves over Q: wild 3-adic exercices, Journal of the American Mathematical Society 14 (2001), 843-939.
K. Buzzard, F. Diamond, F. Jarvis: On Series’s Conjeture for Mod l Galois Representations over Totally Real Fields
Ribet, Ken (1995). “Galois representations and modular forms”, American Mathematical Society, Vol. 32, nº4 (p. 375-402)
By the way, I’m still interested in any info someone can give about the “journal”. If anyone manages to see this comment.
Sorry to cause another bunch of comments from the troll 🙁
————————-
“2) sqrt2 and pi are ill-defined in the new real number system but well-defined in the new real number system.”
E. E. Escultura, “the published one”
http://scientopia.org/blogs/goodmath/2011/01/06/representational-crankery-the-new-reals-and-the-dark-number/#comment-27975
A piece of work is nonsense only to those who do not understand or cannot refute it and that is not my provlem. EEE
How do you know, John when you are not a mathematician?
You are hopeless if you depend on dictionary definition.
So you don’t know that relativity is wrong? It is and this explains why: no publication about it is being published now, relativity has NOT contributed any technology, university programs on it are shutting down and no one majors in relativity now.
Blog posts don’t count in the mathematical world, John.
When a mathematician a mathematician makes a claim or judgment he proves it. Although I have responded to all the questions raised in this site there are still bloggers who cannot see them. I have consolidated my answers to all the questions raised about my work in foundations in my most recent paper, The Resolution of the Great 20th Century Debate in the Foundations of Mathematics, http://www.scirp.org/Journal/PaperInformation.aspx?PaperID=63915
E. E. Escultura
I’ve seen your “counter-examples to FLT”, it consists of about 10 lines of symbol-pushing and could easily be reproduced here. Why don’t you address the point that FLT is a statement about INTEGERS ONLY and you yourself acknowledge that d* is NOT AN INTEGER.
You missed the whole issue. The real number system including the integers is ill defined. Therefore, FLT being formulated in it is ill defined. Then you can proceed from there and understand why the new real number system had to be developed, FLT formulated in it and resolved. EEE
Your formulation of real numbers is ill defined. See Carroll, Mark Chu, 2011, “E. E. Escultura and the Field Axioms”. It is published, Currently under peer review.
Haha, a beautiful piece of self-reference, is this the Gödel approach to handling internet cranks?
XD XD XD I couldn’t resist.
Show why my formulation is wrong. Don’t refer me to others who might be similarly confused. EEE
I already show you. Don’t you know how to use a reference? I obviously can not write the proof here. It is obvious, isn’t it. So I established the falsehood of your proposition.
By the way, if we can be selective about the citations, then ok, but the same rule for both. Show me why reals are inconsistent without referring me to others who are as ignorant as you.
Your game is a bit silly, don’t you think?
Show me where that paper is published. EEE
Reply to John
You are again relying on others. Why don’t you find a flaw in my construction of the new real number system? EEE
Because you won’t show it to us?
ES
> The real number system including the integers is ill defined.
> Therefore, FLT being formulated in it is ill defined. Then you
> can proceed from there and understand why the new real
> number system had to be developed, FLT formulated in it and
> resolved
This is nonsense on so many levels. When it comes to FLT nobody gives two hoots for your “new real number system”: FLT was formulated within the standard system of integers, Wiles’ proof exists within this framework, and it is within this framework that ANY proof of or counter-example to FLT must be formulated.
It’s like me saying I’m better than Tiger Woods at golf because in my own head I’ve changed the rules of golf so that the person with the highest score wins. The fact remains that I’m still not better than Tiger Woods anywhere except inside my own head.
Anyway, there *are* integers in your new real number system, right? So what could possibly be your justification for translating FLT into a form where you allow solutions that, by your own admission, *aren’t even real*?
You still have not understood the issue. Study more and review the posts. EEE
You’re the guy who doesn’t understand that square root is a multivalued function, something any high school student understands, but this is my all *my* problem, yeah.
Reply to John.
I have referred you to original sources and I never rely on the comments of others like you do. On the the counterexamples to the trichotomy axiom and FLT the full discussion is in Escultura, E. E. The new real number system and discrete computation and calculus, J. Neural, Parallel and Scientific Computations, 2009 , 17, pp. 59 – 84. Try to punch a hole on this paper. I can’t punch one in yours since you have published nothing.
On your claim that no one acknowledges my work I refer you to Science Direct where several of my papers in mathematics and physics published by Elsevier Science in the journals, Nonlinear Analysis, Series A: Theory Methods and Applications, and Applied Mathematics and Computation, are listed among the top 25 most downloaded papers and they sell for $31 each (search: escultura, science direct, elsevier science). So you must be seeing things when you look at the scientific literature or just sourgraping. EEE
Ha ha ha, at $31 dollars each download? Mr. Escultura, you should be spending a lot of money in self-complacency!
Would you mind telling us how the number of downloads count as an acceptance of your ideas? I myself have to read some of your nonsense to judge your work. Do them I count as one of your disciples? Please, don’t tell me so!
Cite any paper USING your ideas. If you can not, at least cite anyone not using a limit, complex number, real number, an imaginary number, a… a mathematical idea not denied by you. That will count as some mathematician not dismissing you.
Please, don’t tell us your downloads, you don’t have an iphone game.
And if I am seeing things, and marks, and every person you talk with (you always tell us the same), maybe 7 billion people are seeing things. Maybe those things are reality!
I publish my work in peer reviewed journals, i.e, they are well-defined by by reviewers and that is more than the two hoots that you required. EEE
Both John and ES have blurred vision or don’t understand blog posts right under their noses. John has been making claims he can’t establish. Give me even a single mathematician who refuted any part of my work.
Like Andy you both don’t know what is going on here.
Andy, the counterexamples to FLT required the 25-page construction of the new real number system. What a simplistic mind!!! Or, is it ignorance?
What is the “obvious reason”? Just write down four positive integers, x, y, z, n, with n>2, such that x^n+y^n=z^n. Maybe I am ambiguous, but Fermat was certainly not.
The original source consists of 25 pages! EEE
They must be very big integers.
Mathematics is far beyond integers and computation. You need to learn more. EEE
EEE, you were asked a very simple request. State the four integers to disprove Fermat’s theorem. All Fermat’s theorem contains is integers and computation. You claim to have solved it, tell us the integers you used.
And how are we supposed to learn anything about what you’re on about when you don’t even try to explain it?
Nothing to do with the size of the integers. EEE
Maybe I don’t know how to use citations. Using the journal reference (title and date) that you gave, and searching either the Web or using Google scholar, gives me only portal.acm.org, which is endlessly willing to reiterate the title and provide only the abstract. It’s a fine abstract, but (no surprise) does not contain the axioms.
When I try going to the publisher’s website, the entries for that journal end with 2005.
There’s a question of burden of proof here. You want to convince people that a lot of widely accepted mathematics is wrong. If you make it that difficult, people are going to keep using the math they already know, and spend their free time studying ice sheets or playing with their cats.
Is your goal to convince people that your math is correct? Or is it to convince us, or yourself, that you are smarter and better educated than we are?
I’m prepared to stipulate that (certainly on the education). But Gamow and Einstein wrote books to explain their work to people without Ph.D.s It can be done.
I develop math that I need in science, particularly, physics, biology, geological and atmospheric sciences and physical psychology, not to convince anyone. EEE
Then why are you here?
Reply to Mechanical
The mathematics that I developed for my purposes are contributions to mathematics. EEE
My fierst major publication was the solution of the gravitational n-body problem in, Escultura, E. E. The solution of the gravitational n-body problem, J. Nonlinear Analysis, A-Series: Theory, Methods and Applications, 1997, 30, 8, pp. 5021 – 5032. This was followed by a rapid succession of major publications until today.
Regarding writing for the layman, it is being done in books and chapters to books. One such book is, The Hybrid Grand Unified Theory, Atlantis (a division of Elsevier Science, Ltd, formerly, North Holland), Co-authored with V. Lakshmikanthams and S. Leela, March 2009. It made it to the best sellers’ list of books in all categories distributed by World Scientific in 2009. Made it to the #2 spot in that list in July that year.
Another is the book, Scientific Natural Philosophy, in press at Bentham Science Publishers. It is announced on the Net and in its final phase of publication. More: (1) Extended Geometriccal and Genealized Fractals, a chapter to the book, Fractal Classification and Applications, in press, Nova Science Publishers, and (2) The Big Bang and What it Was, a chapter in the book, The Big Bang: Theory, Assumptions and Problems, in press, Nova Science Publishers. 56 pages.
In the pipeline: Symposium on the Grand Unified Theory, for Nova Science Publishers.
Cheers,
E. E.Escultura
Correction: “Generalized Fractals”
1997? And you’re still waiting for someone to take you seriously?
What an optimistic man!
Reply to John
You’ll never know who take my worke seriously since you don’t know these journals being a nonmathematician. You have only access to cyberspace where the cranks are hiding. EEE
I (a “non-mathematician”, read, unpublished) am currently looking at your paper. Downloaded 0 times in the past year, cited 3 times (by yourself), and with no available abstract. Odd that more physicists haven’t cited this. I mean, I’m not a published physicists, but, isn’t the n-body problem quite tricky?!
You also left no contact information for any of the newspapers likely to want to pick this up! How odd!
Finally, having opened and zoomed into the image provided, I can quite confidently say that the title of the paper in the image, is not the title of the page referring to said image.
ES
Reply to Vicki
All the information you need is in the archives of the publisher. If you want to refute my work it is not my responsibility to go to the original sources.
I have cited my sources, Mechanical; tough luck if you can’t understand them. You probably need some new tools.
Because he has no clue what an integer is.
I advise Escultura again to start reading elementary math books and thinking about mathematics. It will be good for you.
Just don’t start with advanced ones, but with more elementary. Maybe you can grasp the square root concept, and then the imaginary number concept, who knows.
If I were you, I would start with some author with talk a lot about limits, derivatives, integrals, Cantor’s transfinite numbers, the logic behind mathematics, axiomatic geometry, Fermat’s Last Theorem, Gödel’s work and Number Theory, all subjects you openly reject.
A good author who comes to my mind is Hilbert. He worked in all those fields. You can learn a lot from him.
(Yes, Hilbert published, too, and he also contradicts everything yours).
You have not understood the whole discussion here and I don’t expect you to understand Hilbert either. Start from the most basic: mathematical reasoning. EEE
Mathematical reasoning requires logic, which you deny.
What you know is nachronistic logic. To understand what I mean review the posts seriously. EEE
You are misquoting me. I don’t use your defective logic. I use the logic defined by the axioms of the given math system. EEE
Tell us your axioms. We’re still using the old ones, since you can’t show that they have any issues
No, another misrepresentation. My logic and rules of inference are well defined by the given math system. EEE
The axioms define the system, not the other way round. I can see from your statement of the R* “axioms” that you clearly have no idea what an axiom is.
Since you won’t reproduce them here, I have taken your own description from FalseProofs, which is the same as the PDF on your website:
> The rectification is to build a new real number system
> R* with three simple axioms and two operations + and
> x:
> 1) R* contains the basic integers 0, 1, …, 9, and the
> operations + and x are well-defined by
> 2) the addition and 3) multiplication tables of arithmetic
> that we learned in primary school
THESE ARE NOT AXIOMS. They are not even close to being meaningful axioms. The point is to define simple axioms that LEAD to the operations of addition and multiplication. Stating that addition and multiplication are defined “as we learned in school” is utterly laughable.
Look at what MarkCC posted in the original article and educate yourself, you clearly have no idea what you’re talking about.
But them again, it’s not me who thinks your “work” is nonsense. It’s every professional mathematician. Take a look at literature. I’m not standing against you. You are standing against everyone else.
Mention a single mathematician who called my work nonsense. Otherwise, your claim is hollow. EEE
Reply to Mechanical: I have cited original sources, see them. I don’t spoon feed anyone. EEE
As I’ve already said, if you want anyone to bother looking into your sources, you’re going to have to provide something half-solid to show that we should stop laughing at you and start paying attention. Such as, you know, doing ANYTHING worthwhile with your unbroken, yet somehow blatantly broken number system.
And seriously, why are you posting anything here if you’re not wanting to explain? All you do is evade questions and simply state things as though they’re obvious truths, backed up by unrelated gibberish.
No, Mr. Escultura. As I previously said, no mathematician will never acknowledge you in a paper. You don’t exists for science, as you know very well. They have better things to do in their working time.
No, mathematicians will not write a paper calling you a crank. This is not the way it works. They have a better weapon: absolute ignorance. When some crazy guy like you write nonsense they don’t waste their working time writing about them (there are too many like you, sorry). No, they simply ignore them.
Do you want me to name mathematicians who think you write nonsense? Ok, every one of them who continue using limits, real numbers, infinite sums… They ignore your work. If they though your work is valuable, they will revise the foundations. But, hey, take a look at mathematical papers. They’re still using reals!
You want names? As many as you want. Simply look for papers. Here are some of the: Marios Kountouris, Jeffrey G. Andrews, Cédric Pépin, Jordi Marzo, Shahaf Nitzan, Jan-Fredrik Olsen, Jean Bourgain, Sergei Konyagin, Igor Shparlinski, Qinglan Xia, Shaofeng Xu, Yan Dolinsky, Marcel Nutz, H. Mete Soner, Eitan Angel…
How many do you want? I can write as many as you want. You can contribute too, if you know what is a mathematical journal. Take anyone and start reading articles. For any using a limit or a real number or a complex number, write the author. We can get a list from here to the moon.
What you will not find is any paper using any of what you call “your ideas”.
Is this hollow?
And, of course, no mathematician after him understands him. Then neither Hilbert understood himself when he worked on limits, calculus, complex numbers, …
Except you, the published one.
As everyone knows, printers have a mechanism to prevent printing nonsense. That’s why if you’ve published then you’re right. Although everyone thinks otherwise. And while all other publication contradicts you.
This is funny. Ridiculous but funny.
If you are referring to the cranks in SciMath, they have been shut up a long time ago. EEE
Are you implying that Hilbert was a crank by not understand what he was doing? EEE
Hahahahaha! Good joke! Because, it was a joke, wasn’t it? Oh, my, it was not a joke, you can’t read, neither!
No, my cranky cranky friend, I would never say that. Hilbert knew very well what he was doing, and worked very hard.
Hahahaha, you are a little slow, don’t you? Let me tell you, kid’s version.
What I am saying is YOU are a crank because you have not the smallest idea what YOU are doing. You have not see a paper of Hilbert in your whole life.
I’m starting to believe you learnt what you believe are mathematics with Dilbert, not Hilbert.
Reply to all.
Only work published in peer reviewed publications exist and are recognized by the science community. Unpublished ones do not exist and will not make it even to the footnote of history. Any published work that is not refuted stands and is a contribution to the discipline concerned. EEE
Addendum: Unpublished work will have an audience around the watering hole.
Reply to John
Yore mind is trapped in these elementary textbooks the reason you cannot think on your own. EEE
John, I rely on my own research and intelligence. I read the work of others only when I want to know what they are doing. I never copy their work; I cite only when I need them.
Correction: “understand” shlud be “understanding” EEE
A crank thinks everyone else is a crank including Hilbert. EEE
John, you have not given me a single mathematician who has refuted or dismissed my work. I mean, real mathematician, one who has contributed something to mathematics, not a crank.
I think this sourgraping will not get you anywhere. It will only raise your bp. I can sense it in your strange laugh. Stop it for your own good, especially, if you are aspiring to become a matheematician. EEE
BTW, all the papers and books I have been writing since 2008 are invited. EEE
Yes, I have given you a lot of mathematicians who has dismissed your work. They continue using reals, limits, complex numbers, infinite sums, … Is this not dismissing your work? You say reals lead to contradictions. They continue using them. Is this not dismissal? Anyone?
You repeat the question I repeat the answer. Take a (respectable) mathematical journal. Start reading. For any paper you find using reals, limits, complex numbers, etcétera you have find some author dismissing your work. Write them. Now you have the list.
I really CAN NOT write all of them. They will be all the living and dead mathematicians, practically. A random sample: Marios Kountouris, Jeffrey G. Andrews, Cédric Pépin, Jordi Marzo, Shahaf Nitzan, Jan-Fredrik Olsen, Jean Bourgain, Sergei Konyagin, Igor Shparlinski, Qinglan Xia, Shaofeng Xu, Yan Dolinsky, Marcel Nutz, H. Mete Soner, Eitan Angel…
So here you’ve got. Want more?
If you find a real mathematician using any of your ideas, please, don’t be shy, let us know.
” I have given you a lot of mathematicians”. You must be dreaming. You need to give me JUST ONE NAME and a reprint of his PUBLISHED work on the subject and I’ll respond to it. EEE
You only dropped names which are quite impressive but you have not given me a single mathematician who refuted my (published work). Published work is accepted by reviewers who are mathematicians. You are playing a silly game. Other cranks have better sense. EEE
It’s easy to drop names, John. Give me me just one living mathematician who refuted my work.
We have all read Martin Gardner in our youths, and we know about the history of perpetua mobilia, so it is clear such characters have always existed and will continue to flourish. But such a perfect example makes one wonder! Could it be that our guest is impersonating Escultura? Is it conceivable that the man is MarkCC’s literary creation? His doctor Matrix, with publications and all? Having Escultura here seems to be a successful blogging strategy, what with such a comment thread! But no, it must be the real man, who can’t resist having the last word on each and every sub-sub-thread…
Only one who knows has the last wordd, quim.
I have had enough of this Mr. Escultura.
The guy says limits are nonsense, I refer him to the work of Weierstrass and he says he doesn’t read “other people”‘s work, he do his own mathematics. Then he says people call nonsense the things they don’t understand, and that we are forced to read his “work”.
Too much irony. Anyway, here there is already enough information for anyone to judge himself. Besides, I have been posting a little too much on this.
But I’m still curious about something, and have some questions.
What do you people know about the journal, “Neural, Parallel and Scientific Computations”? I know a lot of scientific journals, but follow only a couple of them. And I have never heard of this one before (which doesn’t mean anything, of course, I’m only asking. Even reputable journals have its own Bogdanovs or unintended Sokals).
What kind of journal is it? What reputation? How many subscriptors? What kind of authors? Is it really peer-reviewed? Who are the frequent reviewers? What is its story? Who are the editors?
Does anyone here know about it?
Like most journals I publish my work in, Neural, Parallel and Scientific Computations is new, peer reviewed and updated and published by well established and renowned publishers, in this case, Dynamic Publishers. A large number of my publications appeared in Elsevier Science, Ltd (fomerly, North-Holland), a world renowned publisher. Of course, non-mathematicians never heard of them.
I tell you John, your sourgraping will not get you anywhere. Bye.
Cheers,
EEEscultura
To John:
The present limit in calculus is nonsense for reasons I have stated umpteen times. Limit point in topology makes sense. My g-limit in my mathematics is the appropriate concept in my work.
BTW, where is the name of the MATHEMATICIAN who refuted my work, John?
If you don’t know these journals, you must be living in the Middle Ages.
Yes, you have posted a lot none of which you have established or substantiated.
This name dropping is impressive, John, but does you no good. Why don’t you go fishing and relax or prepare for your class to teach wrong mathematics?
Dr. Esculutura: How did your Nobel Prize nomination work out? (in Physics, I believe you have said). Any updates or travel plans to Stockholm.
Reply to Dave,
I believe you were one of those sourgrapers who prayed and hoped that my nomination was a hoax and I congratulate you for having survived the great disappointment. Like the Nobel Peace Prize the Nobel Prize for Physics is a formidable political institution. The latter, in particular, is controlled by a certain group. You can identify that group by finding out what is in common among the majority of the winners of the Nobel Prize for Physics since the 1970s. The ones who trumped up a false charge aganst me that was used as an excuse for the Selection Committee to award the Prize to three other physicists despite the fact that I got the highest number of votes from the Swedish Royal Academy of Sciences belong to this group. The winners for that year, 2005, belong to this group. You will recall that the eminent scientist Gerholms resigned from the Selection Committee in protest. The latest confirmation of my nomination is the announcement of my book, Hybrid Grand Unified Theory (published by Atlantis, a division of Elsevier Science, Ltd, March 2009) by the distributor, World Scientific, which specifically mentions my nomination. BTW, the book made it to the best sellers list among books of all categories in the natural and social sciences and got to No. 2 spot in the list for July that same year. Thus, your question could have come only from a crab but you remain unscathe behind your username. EEE
I got this comment off an old website that reviewed Dr. Escultura’s statement that he was nominated. This is from September 2006 and I found it interesting:
“So even if there is a real Prof. Gerholms out there somewhere, and even if he had some role in selecting the Nobel Prize winner in Physics, this story is not credible. For one thing the Nobel nominations are secret. Only the winners are revealed. Not even the other nominees themselves know they were nominated. It is not credible that someone on the selection committee would be so unprofessional as to violate a confidentiality agreement by revealing the names of any other nominees.”
Here’s a link to the post, in case I’m taking this out of context:
http://dontletmestopyou.blogspot.com/2006_09_10_archive.html
as well as another interesting post on the same blog from the year before:
http://dontletmestopyou.blogspot.com/2005/06/escultura-still-riding-dead-horse.html
If this has already been discussed in the comments above, my apologies, but I didn’t remember seeing it mentioned previously and thought it was possibly germane.
Paul Hawking
Blog:
The Challenge of Teaching Math
Latest post:
I get what you’re going through
http://challenge-of-teaching-math.blogspot.com/2011/03/i-get-what-youre-going-through.html
Here is a recent article on my nomination:
http://bmhegde.com/hegde/articles.php?article_id=198.
Another one is the introduction to my book, Hybrid Grand Unified Theory, by World Scientific. By the way, this book was a best seller in 2009 among books published by this publisher. It was #2 in the list for July that year.
You accuse others of sourgraping, then whine about how you totally deserved that prize, but there’s totally this organisation that are totally like biasing the process.
I mean seriously?
Reply to Paul Hawking
Yes, this blog, Wikipedia Encyclopedia and a third one are the only blog and websites that tried to discredit my work without success (they also eventually blocked my username from posting when they ran out of gas) because there are hundreds of blogs and websites which are objective that allowed free expression by all parties with different perspectives on my work. If you broaden your myopic vision you will see them. EEE
I never whine about anything, Mechanical. I never even expected the prize because this organization, like all other institution of this kind, is controlled by a group. You can identify the group by analyzing the winners during the last half century.
The Nobel Prize organization’s legal department may be very interested in the book.
I don’t know if they actually enforce fair use of their brand, but it will be very interesting to find out.
Reply to Mechanical
I never whined about the Nobel Prize because I knew the outcome since like the Peace Prize this institution is political and controlled by a group. EEE
Reply to John
Would you bet the legal department will hid your advice?
You are, again, imagining things, John. The announcement of the publication of my book simply mentions that this author was nominated for the 2005 Nobel Prize. What has the legal department to do with it? Sourgraping, isn’t it?
Reply to Dave
Visit this: http://bmhegde.com/hegde/articles.php?article_id=198.
I think it is time to conclude and summarize this debate on cranketry.
1) A crank cannot be a mathematician or scientist (published in peer reviewed scientific publications). The latter may err but no one calls him crank except a crank. For instance, Einstein erred but no one calls him a crank. A scientist or mathematician may err because scientific knowledge is not sufficiently advanced to expose the error. However, when scientific knowledge advances sufficiently such error, if any, may be revealed.
2) Where then do we find the cranks? Naturally, in cyberspace, where they can make pretensions by bluffing, dropping names and expounding on something they know nothing about or hide behind usernames.
Bye folks.
Cheers,
EEEscultura
QUOTE by Escultura:
“A crank cannot be a mathematician or scientist”
No. Georg Cantor was a crank (with respect to Francis Bacon as Shakespeare). Isaac Newton perhaps qualifies as one of the largest cranks the world has ever seen (his interpretation of Judeo-Christian literature, perhaps his alchemist work also). You think just because is a mathematician or scientist they have some magical power which prohibits them from believing in some ridiculous idea *and then stubbornly sticking to it even in spite of conflicting evidence*? It doesn’t. And I do call both of them cranks.
Then a nonmathematician Doug Spoonwood is a crank with respect to mathematicss. EEE
If you take my comment here as evidence of such, then you’ve committed a fallacy of irrelevance, since who is/who is not a “crank” doesn’t bear on mathematical knowledge. Try constructing a real argument E. E. Escultura.
To Doug Spoonwood:
I am referring to mathematicians or scientists, not religious believers which is outside my expertise.
A mathematician can be wrong due to inadequate knowledge during their time but they are serious and know their stuff, Doug. Certainly, they are not bloggers.
Suppose Adam declares, “The measures of the interior angles of a triangle in Euclidean space always add up to 180 degrees.”
Suppose also that Ben announces, “Euclidean geometry is ill defined,” then constructs a triangle on the surface of a sphere, and shows that the sum of its interior angles is not 180 degrees.
Is Ben’s construction really a counterexample?
Your FLT counterexample relies on an isomorphism from the integers to the decimal integers. Otherwise you could not present d* (not an integer) and 0.999… (not an integer) in your counterexample to FLT (which is constrained to positive integers). Rather slippery.
But you state in your paper that d* “behaves like 0 and 0.99… like 1”. Consequently the triplet you present as counterexample behaves like
((1)(10^T), 0, 10^T).
The second element in the triplet does not “behave” like a positive integer, and thereby behaves like a disqualification.
Reply to bibliovore
Understand that a mathematical space is well defined only by a CONSISTENT set of axioms. Short of this you have nonsense.
I did not rely on the isomorphism between the integers and the decimal integers. I PROVED IT.
Unless something new and sensible is posted here this is my last. EEE
The discussion is interesting, but a bit above my head. However, I would like to commend EEE for the above. And congratulate him on his patience, even if it was repaid with rotten tomatoes.
When James Clerk Maxwell published what became known as Maxwell’s equations, not a lot of his “peers” bought it. But he had enough of a reputation that most others were polite to him. He also had to plow the field with ~”ox and alongside ass,” because he used vector calculus, which many of his peers could not follow, so he also used triples of his equations (one for each axis). Even then, it took awhile before most of his peers caught on.
I believe you’ve got your history facts wrong, Mr. Wallace.
Maxwell was highly acclaimed for his work on electromagnetism (and for almost all his work, in general). He published his theory in 1873, it was reformulated in 1881 by Heavyside (a mere 8 years later), and it was verified experimentally in 1886 by Hertz after many trials. They were working hard on it, and they invested their time on it.
Maxwell didn’t use vector calculus. He was a follower of Hamilton and his quaternion calculus, and he formulated his equations in terms of quaternions. The theory was reformulated into vector calculus by Heavyside and others.
Where did you read all that?
Apart from that, I don’t see the similarities. You are comparing a physical theory (which can not be proven right) to a mathematical work (which can). They are not comparable.
Even if you don’t rely on this, I don’t see the situations comparable at all. Maxwell gained a string reputation for his works, never said everyone before him were wrong (which Egdar says), he never said well established concepts are nonsense (which Egdar says because he doesn’t know how to operate with imaginary numbers, limits, …), he didn’t claim to have a recognition he didn’t have (which Egdar says; he claims to have been nominated to a Nobel Prize!).
Now that the Nobel Prize organization knows about his published false claims on a book, which he made for commercial purposes (to have any probability of selling a book), I expect them to enforce him to withdraw the book. Then we’ll see this is not a matter of opinion. He is actually publishing wrong things for lucrative purposes.
Reply to John
I have no plan to withdraw a book in the best sellers list for 2009 and in the #2 slot of that list for July 2009. At any rate, I am aware that one who can’t do mathematics is often deflected to do history of mathematics instead. Thanks, William. EEE
Yeah, I did some additional research and found the Nobel prize nomination claim. I couldn’t confirm he was actually nominated, but it seems incredible.
Regarding Maxwell, yes, I should have known better than to say vectors instead of quaternions. They are very close, however, in context, no?
I’ve gotten a lot of my information from memory, after reading Basil Mahon’s “The Man Who changed everything.” I just checked, and I think you’re giving more credit to others vis. a. vis. Maxwell than Mahon, who write:
Also, I calculate 1864 to 1888 from presentation to Hertz famously setting out to experimentally verify Maxwell’s predictions. Small matter, but the dates differ from yours.
Anyway, I retract some of my comments regarding EEE. I commend him for engaging the opposition, but it appears upon further reflection that his engagement is superficial at best.
Regarding Maxwell, I still think the scientific community was slow to accept some of his greatest work. There are many reasons for this (e.g., unlike Darwin, Maxwell had no T.H. Huxley using his theories to goad Christians, thereby bringing them to the attention to the masses).
Nonmathematicians can only dwell on the surface of the discipline as they have no access to peer reviewed publications. EEE
Incidentally, it looks like Basil Mohen also wrote a book on Oliver Heaviside. I’ll be checking that out, too.
Thanks for dropping the name.
Ah Escultura, still at it I see. I remember having discussions with this fellow back in 2005, when much stuff about him was written in the Manila Times, including this gem, on the front page no less:
http://replay.waybackmachine.org/20051217110937/http://www.manilatimes.net/national/2005/jun/19/yehey/main.html (had to use webarchive, since the Manila Times archives don’t go back past 2008)
Escultura is as dense as they come, although the lack of fact-checking from The Manila Times journalists is incredible (I think Escultura was somewhat of a co-editor at the time, yet it’s still amazing that they let him post his bullshit in their newspaper). IN FACT, they even state here:
http://replay.waybackmachine.org/20050514073617/http://www.manilatimes.net/national/2005/may/10/yehey/opinion/20050510opi8.html
that their source of information was Escultura himself, and that they “did not have any reason to doubt him”.
There were several more articles in The Manila Times, a few containing “personal letters” to Escultura from, among others, Wiles, Hawking, and members of the Nobel Committee. Here is the first such instance:
http://replay.waybackmachine.org/20050514021451/http://www.manilatimes.net/national/2005/may/05/yehey/top_stories/20050505top4.html
Of course, they weren’t actually personal letters, but merely guestbook entries:
http://htmlgear.tripod.com/guest/control.guest?u=eescultura
(There was also a forum which contained much more discussion, but I can’t find it). Of course you could sign the guestbook as anyone that you wanted to, and Escultura (and, in turn, The Manila Times) would think you were legit. Unless, of course, you disagreed with Escultura, in which case you were an imposter.
The guestbook link doesn’t seem to work, hopefully this one does:
http://htmlgear.tripod.com/guest/control.guest?u=eescultura&i=1&a=view
Glad to see you here Gareth. How did you get off the pit I left you in four years ago? Have you added sqrt2 and sqrt3 yet? Maybe John can help you. EEE
The result is irrational. Can you explain why you keep going on about it? Irrational numbers are perfectly valid.
Probably because it’s the only mildly valid statement he’s made this whole time.
And I use the term ‘mildly’ and ‘valid’ very loosely.
And then, of course, there’s the fact that he can’t do it either, he’s just trying to claim that our form of maths is incorrect because it recognises sqrt(2) as a number. Of course, without being able to use square roots of non-square numbers, any equation or algorithm using square roots goes completely out the window. And heaven forbid that someone should try to use trigonometry!
Right and what is the result? Write it. EEE
Because the sum DOES NOT EXIST, Andy. Did you get it?
You missed the point, Andy. I only stress the point that nonterminating decimals cannot be added because they are ill-defined in the real number system. Their sum can only be APPROXIMATED by a terminating decimal.
Where is that subpoena from the legal department, John?
This is essentially a discussion about real numbers, and what I’m missing in all the comments is a clear explanation of how they are defined. So I thought I’d give my view on this, and in the process answer EEE’s question of how to add
and 
.
Real numbers are (in one of many definitions) defined as equivalence classes of Cauchy sequences of rational numbers. A sequence
is Cauchy if the difference of terms can be made arbitrarily small: 
such that 
.
Two sequences are equivalent if their difference converges to zero.
Now to identify a real number it is sufficient to identify a single sequence in the equivalence class. When we say 0.3333…, we mean the sequence {0.3, 0.33, 0.333, …}.
To describe
we need to find a sequence such that the squares of the terms converge to 2. This can for example be done by solving 
using Newtons method:
One can prove this is a Cauchy sequence, and
, the rate of convergence can also be calculated. This identifies an equivalence class of Cauchy sequences which we call 
. If we wanted to know the nth digit in some base B, we could iterate this sequence N times until the difference in terms after the Nth is less than 
, so one could say that ALL digits of 
are known (tell me which one you cannot calculate!) Similarly for 
,
Now if we want to add
and 
we would just need to add the terms of these two sequences 
, this identifies the equivalence class of Cauchy sequences which we call 
. Alternatively you could use Newton's method to find a solution near 
to 
to find another sequence in this equivalence class.
The fact that a number is irrational is not a problem as long as you can find a sequence converging to it. Of course the above story is a technical matter which most mathematicians learn somewhere in the first or second year at university and then promptly ignore (or forget) for the rest of their career as it is much simpler to just write
.
Excellent post. EEE claims that:
> “A real number is well-defined if every digit is known or computable.”
and then inexplicably goes on to conclude:
> “Therefore, only the terminating decimals are well-defined.”
Although he goes on to claim that pi and e are exempt because there is an algorithm for computing them, he consistently ignores the fact that there is obviously an algorithm to compute any digit of sqrt2, or (sqrt2 + sqrt3) , or even more trivially 1/3, which he also claims to be ill-defined.
“If we wanted to know the nth digit in some base B, we could iterate this sequence N times until the difference in terms after the Nth is less than B^{-(n+1)}”
If you calculate to the Nth iteration with this prescription are you sure you will have the first n digits correct? I’m skeptical. What if you’re using decimal and you calculate the nth digit as 9?
Ah yeah, if the nth digit is 9 and the (n+1)th digit would be a 9 as well this wouldn’t work, since the maximal error is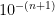
so it might be possible that this changes a digit. Replacing n+1 by n+2 or higher won’t solve it either, since there could in theory be a whole string of 9s there of unknown length. See for example the sequence converging to 1, {0.9, 0.99, 0.999,…} By calculating a specific N digits, you cannot know whether your sequence converges to 1 or to 
or anything in between.
The point still remains that you can estimate your real number by a rational number to any accuracy desired.
Yeah but Escultura requires that each digit be computable. So in order to show that a real number is “Escultura-well-defined” you apparently need to show that for each digit there exists an algorithm that will stop in finite time to compute that digit (assuming that’s what he means by “computable”). I think you can still do that … you just need to modify your proposed algorithm slightly. Note that only rational numbers have decimal expansions with an infinite sequence of 9s.
Probably, although I don’t see the correction immediately. One also needs to be aware of numbers such as 0.9099099909999… which has arbitrary long sequences of 9s but is (I think) not rational.
Thats all besides the point though, nothing in the definition of a real number sais its digits must be computable.
I was just trying to point out how you could modify what you had above to give a proof that for example sqrt(2) is “Escultura-well-defined” according to the definition:
“A real number is [Escultura-]well-defined if every digit is known or computable.”
I interpret “computable” as meaning that there exists an algorithm that will output the digit in a finite amount of time.
You’re right that 0.9099099909999… (extended in the obvious way) has arbitrarily long runs of 9s, but for any particular digit there are only a finite number of 9s after that digit before a zero.
I would not call those numbers “Escultura”-well-defined.
On one hand, he does not accept most of them as valid. For example, as you have pointed out, 1/3.
On the other, that kind of numbers already have their own name: they are the set of computable numbers. However, not every real is a computable number. Well, most are not even definable!
Regarding the infinite sequence of 9s, in practice the problem can be almost always solved by bracketing. I mean, to compute sqrt(2), you start by
1^2 < sqrt(2)^2=2 < 2^2
So you know your number is between 1 and 2, and, as sqrt(2)^2 2^2, you know it is not 2. So the first digit is 1 for sure. Then you can continue.
1.4^2 < sqrt(2)^2=2 < 1.5^2
As sqrt(2)^2 1.5^2, you can now be sure the second digit is 4. If you can bracket the number, you can tell if your sequence of 9s will end. Because, otherwise, the right estimate would be equal to the formula you use to find your number .
Of course, as most numbers are not computable, you can not always apply this procedure.
The test of clarity of algebraic operation is in writing the result. Now, write the result of adding sqrt2 and sqrt3. BTW, only a terminating decimal has algorithm for computing its digits in FINITE TIME. (For the resolution of this question and more clarification, see Escultura, E. E. The new real number system and discrete computation and calculus, J. Neural, Parallel and Scientific Computations, 2009, 17, pp. 59 – 84) EEE
EEE,
1/3 = 0.3333… is a non terminating decimal. Which of its digits CANNOT be calculated in finite time?
The algorithm for calculating the digits of o.33… is sustained division of 1 by 3 and you cannot calculate all of them. The same applies to e and pi using their infinite series expansions. Do you know what the algorithm is for calculating the digits of 0.99…?EEE
The algorithm for calculating the nth digit of 1/3 is:
Thats it…
It terminates in finite (very short) time for every n. Thus all digits of 1/3 can be calculated in finite time. I ask again, since you claim that not all digits can be calculated, for which n does the above algorithm not terminate in finite time or give the incorrect answer. None!
This is a completely irrelevant point though, the definition of a real number does not even require that its digits can be calculated.
Sooo… e and pi no longer exist either?
Mechanical: well they do in base e or pi, obviously…
BTW, pi is non-terminating. As is e. Why are they exceptions?
Already answered above. EEE
Yes, Dr. Escultura has already answered this question. In his March 23, 2011 at 11:34 am post, he says:
“The algorithm for calculating the digits of o.33… is sustained division of 1 by 3 and you cannot calculate all of them. The same applies to e and pi using their infinite series expansions.”
So he is saying that e and pi (like 1/3) are also not well-defined.
(Yes, he contradicts himself. Yes, many people have already discovered this and pointed it out to him repeatedly. No, he won’t admit it. Yes, people have discovered that they are wasting their time talking to him. Yes, this will be my last post here.)
Now, please write the sum, Robert, like 2 + 2 = 4. You just re-wrote the left side of your binary operation +.
Robert, I have no problem with your definition but you did not disput what I raised: that nonterminating decimals cannot be added. Their sum can ONLY be APPROXIMATED. You only added sqrt3 to sqrt2 but you did not write the sum.
If you read more about Escultura, you’ll find that he has a problem with the existence of i (where i^2=-1). He gives the following as his “proof”:
i = sqrt(1/-1) = sqrt(1)/sqrt(-1) = 1/i = i/i^2 = -i
People have told him that sqrt(ab) = sqrt(a)*sqrt(b) only if a, b>0, but unfortunately he doesn’t listen.
Let me present an “Escultura proof” that the number 1 is problematic:
1 = sqrt(1) = sqrt(-1*-1) = sqrt(-1)*sqrt(-1)=i^2=-1
First, it’s nice to have an entry in cyberspace from that part of the globe. Having said that, I want to point out that I have responded to your question in many websites. In particular, see URL http://falseproofs.blogspot.com/2006/06/e-e-escultura.html. I’ll not repeat my response here but I remind you that the operator sqrt is ill defined when applied to a negative number such as -1. In other words, sqrt(-1) is simply nonsense and this is the source of the above contradiction. Finally, I remind you that mathematics is much more than listening, manipulating symbols and book learning; it requires deep thought and ridding it of anachronistic ideas.
Cheers,
E. E. Escultura
You seem to be arguing from your conclusion: “the square root operator is ill-defined on negative numbers, which I will use to manipulate it in odd ways and get a contradiction, which proves that sqrt(-1) is ill-defined.”
Reply to Vicki
Could you state your definition of sqrt(a)? Perhaps, we are referring to two different things. EEE
Way to completely ignore Vicki’s point.
sqrt(1/-1) = sqrt(1)/sqrt(-1)
is NOT true, since sqrt(ab) = sqrt(a)*sqrt(b) only if a, b>0
You justify writing this incorrect statement by claiming that sqrt is “ill defined”, but your only justification that sqrt is “ill defined” comes from incorrectly deriving the contradiction
i = sqrt(1/-1) = sqrt(1)/sqrt(-1) = -i
It actually doesn’t matter what your definition of sqrt is, this is a completely circular argument on any level.
Anyway the definition of i is not i = sqrt(-1) but i^2 = -1, so even if you demonstrated a problem with writing and manipulating “sqrt(-1)” (you haven’t) then you still wouldn’t have said anything about imaginary numbers.
Reply to Mechanical
“Calculating a number” is different from “writing a number”. The infinite digits of a nonterminating decimal cannot be calculated in finite time. That is why a nonterminating decimal is ambiguous and cannot even be written precisely on paper; it can only be approximated within a desired margin of error. Perhaps, you will understand what I’m saying if you try to write the exact sum sqrt2 + sqrt3. EEE
Reply to Andy
You have not defined i but you are using it in your arguments. I dismiss it as nonsense being ill defined. Howwever, if you well define it we can have a sensible discussion. EEE
I did define i in my last post.
i is defined by i^2 = -1
If a number cannot be written down exactly (as a sequence of digits in some base) just because you will run out of paper, does not mean this number is not defined, ambiguously defined, or whatever. As long as you have a way of approximating the number to any accuracy desired (for example by the methods I described in a previous comment) the number exists.
If I would want to write the exact sum of two square roots, I simply write
. This uniquely identifies the number I wish to work with.
If I would want to calculate an approximation to this sum, I would use Newton’s method.
I see no problems there…
I suspect Escultura redefines the real numbers as “those numbers you can write down”, or something similar. This is not the set of real numbers as most of us understand them, and it would not surprise me if his definition is indeed ill-defined, inconsistent, and has a whole lot of other problems. All good reasons not to use that definition!
Reply to Andy,
The exponential operation, in particular, when the exponent is 2, applies only to or is defined only on real numbers and there is no real number whose square is -1. Therefore, your defining equation for i is vacuous and i is ill defined, nonsense. EEE
EEE, that’s the weakest objection you’ve come up with yet. You essentially just wrote “You cannot define the square of i because the square of i is not defined.”
*The square of i is defined as -1*. Just think of it as our new axiom that extends the reals to the complex numbers, since you’re so obsessed with the concept.
Reply to Mecanical
I don’t care what else you do, just write the sum of sqrt2 and sqrt3 to dispute my statement.
Andy, the problem starts with the nonsense sqrt(-1) and everything I wrote comes from it.
Maybe you should try to write the exact sum of e + pi… I think you’ll find you have the same problem
Reply to Robert and Mechanical
That’s what I have been saying all along, that a nonterminating decimal is ambiguous because you cannot compute it completely. You can only approximate it up to desired margin of error. This applies to e and pi. This type of ambiguity is what I call contained. All well defined nonterminating decimals, i.e., decimals for which there are algorithms for computing their digits, are contained. EEE
So let me get this straight…
e and pi are irrational numbers
sqrt(2) and sqrt(3) are irrational numbers
1/3 and 1/7 are non-terminating, rational numbers
All six of these numbers have several algorithms to compute them.
While it’s impossible to write any of the above numbers completely in decimal form, it’s entirely possible to represent 1/3 and 1/7 completely in decimal form, and it’s child’s play to work out the value of any decimal place of these numbers.
For sqrt(2), sqrt(3), pi or e, we need to either resort to approximations or write their word or symbol approximations.
However, pi and e you don’t have issues with, because they can be approximated by an algorithm to a desired margin of error. sqrt(2), sqrt(3), 1/3 and 1/7 can all be approximated equally well, but they don’t exist.
Indeed, in 1/3 and 1/7’s case, there is absolutely no limit to the number of decimal places we already know. For example, I can tell you off the top of my head that the 9,423,268,362,851 th decimal place (far further than anyone would ever need to know) of 1/3 is a 3. The same decimal place of 1/7 is a 5, using a calculator and ~15 seconds of my time. I imagine that finding the same decimal place of pi or e would take substantially longer.
Is that an accurate summary? If not, I hope (again) to see the algorithm you use to calculate pi, so I can attempt to produce an algorithm to calculate one of the other numbers using identical logic.
And don’t point me towards a source, it’s good fun talking about this, but not enough to invest any more than a little time into it.
To Angelito Salenga:
Tell me what’s wrong with my proof; don’t give me a wrong example.
More on Robert
Mathematicians often see problems that amateurs cannot. EEE
You said this the other way around, not too long ago…
“it sometimes happens that the layman can see much further than the experts” ~EEE
Yes, that is right. But the experts can see much deeper than the amateurs who can only dwell on the superficial. I think I have said this before also. EEE
More reply to Mechanical
It’s child’s play to APPROXIMATE the value of any decimal. It’s IMPOSSIBLE to work out the value of any nonterminating decimal.
An approximation of a nonterminating decimal IS NOT THE SAME AS THAT DECIMAL.
Fractions and decimals are different number systems. There is only 1 – 1 correspondence between them. You can consider fractions as ordered pairs or you can consider them as quotients expressed as decimals. They behave differently with respect to addition and multiplication.
I can approximate pi from its series expansion and even write a finite number of its digits as nonterminating decimals.
I don’t need any source for simple arguments like this.
EEE
So to how many decimal places do you need to accurately go to before your approximation of pi is valid? What algorithm do you use to approximate pi? The only algorithms I’ve seen use values that you claim we can’t use, I’d be interested to see one that relies solely on whole numbers and dividing by 2 or 5
You can always approximate pi (or any well defined nonterminating decimal) by its initial segment of terminating decimal, say, at the nth decimal segment and the error will not exceed 9(.1)^n. This is valid but is not the only valid approximation. What is impossible is KNOWING THE EXACT VALUE of pi or any nonterminating decimal. EEE
If you don’t know the exact value, then what do you mean by error? Presumably the error is the difference between the approximation and the exact value, right?
I can not believing you’re still arguing with him. Well, yes, you’re in your right to have fun with the troll and debunk him. I’m not talking about your rights. I’m arguing about your patience.His arguments are more lame every time he posts.
After he challenged you to find an algorithm for computing the digits of 0.9999… (where every digit is 9, oh, how difficult!), thinking you will never find one, I thought I read one of the most stupid things ever. Then he came up not knowing how to operate with the imaginary number in an elemental way. He says you can only use axioms to infere. What axiom did he use to write i=sqrt(1/-1)=sqrt(1)/sqrt(-1)=-1? What axiom did he use to assert there is no number i which makes i^2=-1, having one axiom saying this?
And now you’re arguing with him if sqrt(3)+sqrt(5) an be accepted as a valid number despite not having a complete decimal representation.
Come on! Can oneone here wrie a complete decimal expression for d*=1-0.999… which makes d*>0? If we don’t accept in a system any number lacking a complete decimal representation, then how can we accept d*? Because d* is an axiom? We have axioms for sqrt(3)+sqrt(5), and this is an exact value, and we can exact series representing the sum, and we can operate with the number in an exact way:
x=sqrt(3)+sqrt(5)
(x-sqrt(5))^4 = 9, which is exact
Because d* is defined by an expression? So is sqrt(3)+sqrt(5). Why then it is silly sqrt(3)+sqrt(5) and not d*=1-0.999….>0?
I believe you should not answer any more of his posts until he proves
d*=1-0.999….>0 can be written in exact decimal form
or
he accept numbers are valid even if they lack a complete decimal form
But then again, this would be as expecting he to explain what his concept of continuity is, knowing for example the function
f(x)=x*x-2
makes f(1) negative, f(2) positive, but he asserts there is no number between 1 and 2 which makes f(x) zero. Good bye, Bolzano.
Then you can ask him why the Banach-Tarski is a contradiction (tip: it is not); why a limit is an ill defined concept, and how can PI be ill defined in decimal form, if PI is not defined as a concrete decimal expansion (PI is not defined as 3.1415…, this is plain silly), but as the ratio between the circunference and the radius of a circle under an Euclidean metric; why do he falsely claims he was nominated to a Nobel prize, when he wasn’t (putting his publisher into trouble); why he claims his book to be a best seller when anyone can see its ridiculous position in amazon (tip: I couldn’t find a book less sold); or why he likes so much ridicule.
Can anyone here write d*=1-0.999….>0 completely in decimal form without making a mistake?
Can anyone here write the axioms that justify writing i=sqrt(1/-1)=sqrt(1)/sqrt(-1)=-i?
He asserts without proof that 1/3, sqrt(2), pi and e are “ill-defined” in the real number system, but I think there is a second part to his “new real number system” where he suddenly realises that he has constructed a completely useless system and hand-waves non-terminating decimals back in. I really don’t follow this part, some garbled nonsense about “accepting there is an error”, et voila, non-terminating decimals are now well-defined in R* basically because he says they are.
You’re right though John, it was fun for a while but when someone thinks that writing “3) the multiplication tables that we learned in primary school” is in any way an axiom of a formal system then it’s time to call it a day.
Not being a mathematician, Andy will never understand any article in any peer reviewed international journal.
Why are nonterminating decimals ill-defined IN THE REAL NUMBER SYSTEM?
ANSWER: None of the binary operations of the real number system applies to them. Try the sum sqrt2 + sqrt3 and WRITE THE ANSWER HERE:
Andy, I never claim that that I can add e and pi; I can only approximate their sum.
Robert, I can give you a trillion pieces of paper and even allow you to use a computer. Still, you cannot write the sum.
SeanH, I can approximate the exact value because I can approximate the value of the tail end of a nonterminating decimal.
I think EEE might just be the most applied troll I’ve ever come across. I rate you 8/10 sir, for effort.
Since EE Escultura wants to comment here, and never tried to point out any inconsistency in Mark’s definition I may as well try to do so. First off axiom 6 needs to say “exists” in a key spot
“Multiplicative Inverse: For all a in F where a ~= 0, there *exists* a multiplicative inverse a^{-1} such that a * a^{-1} = 1.”
Now that’s just a typo. However, one might and try to argue that “for all” has to quantify over *all* members of the domain of discourse. Consequently, axiom 6 isn’t consistent (with such an understanding of predicate logic), since the clause tries to make it so that we have a quantification over all members of F, except one member of it. Quantification having to happen over *all* members of the universe of discourse, and then actually happening over all but one of them is not consistent, since “almost” all is never all. One could continue that this really means that a field doesn’t consist of one collection of values F, but rather two collections of values F and F’. For F we have a commutative group for addition, distribution of multiplication over addition, and a commutative monoid for multiplication. For F’ we have a commutative group for multiplication, distribution over addition over multiplication, and a commutative semigroup for addition. To call a field a single collection of values, in this way, also comes as inconsistent.
Edit: Addition isn’t definable for F’ (where F’=F-0), since for for F’ we have a commutative group for multiplication. Note that the structure of F’ differs from that of F since multiplication differs.
One of my criticisms of Mark is quite simple: He applies an operation in the real number system to an object which is not a real number. That is nonsense. It’s like playing a game of chess and taking a piece on the checkerboard.
Just curious Doug, what is the decimal multiplicative inverse of 7 so that its product with 7 = 1? Show the proof in detail.
Pretty sure EEE is trolling you all, guys.
I have not been here for sometime and as I expected, a lot of nonsense has come up. Let me just take on a nonsense of John.
He is asking about the decimal expansion of d*.
Until now he does not know that d* is not a decimal? It is not even a real number and yet he raises the question of accepting it as a real number. He uses d* as if it were a real number. Its like playing a game of chess and taking a piece on the checker board. Even a two-year-old won’t do that!!!
Where is your answer to sqrt2 + sqrt3, Andy?
I wish someone writes down just one correct refutation of my work by the bloggers here. At any rate, thanks folks; it has sharpened wits.
Correction
… it has sharpened MY wits.
Really people, we need to stop giving this crank a soapbox to preach from. I’ve seen quite a few blogs that give concise and simple refutations of Esculturas “theory”. Sure enough he finds them (how much time does he spend googling his own name???), and without missing a beat hijacks the comments section and turning it into his own private soapbox. Many many people (myself included on another blog) have attempted to demonstrate to him that he is wrong, and it never sinks in. You come back to look at any new comments and you find that Escultura himself has posted ten new ones.
There is no point in arguing. Let the old man enjoy his delusions of grandeur. The more people that argue with him the more important he feels, as he actually believes that he has proved us all wrong then posts comments like:
“I wish someone writes down just one correct refutation of my work by the bloggers here. At any rate, thanks folks; it has sharpened wits.” -E. E. Escultura
I myself demonstrated more that one refutation to his claims, but then he changes the rules. At one time d* is a real number, then it is not, then it is, then I’m breaking the rules by “mixing systems”, the excuses never end.
Maybe if we just ignore him he will go away.
Show me just one argument against my work, D, and I’ll show step by step that it is nonsense. Then you can rebut, etc.
Addendum:
I bet you can’t do it, D, because not even a single mathematician has punched a hole in it.
The classic mark of a crank: “Nobody’s punched a hole in my argument” especially when your argument is complete nonsense.
By “my work”, Shadonis. I mean, published work. Only mathematicians can possibly punched a hole in it, not bloggers who are not mathematicians.
No mathematician cares what you’ve written. You’re simply wrong; your “system” is useless; and you’ve never been nominated for a Nobel Prize. Never.
Write one argument against my work, D, and I’ll show step by step that it is nonsense. Then you can rebut, etc. My sense is, no one here is capable of putting up a valid argument against my work because not even a single mathematician has found a hole in it. I know John has been trying hard to find such mathematician but failed. That’s why he ran away. I drop by between work occasionally to relax and amuse myself.
Write one argument against my work, D, and I’ll show step by step that it is nonsense. Then you can rebut, etc. My sense is, no one here is capable of putting up a valid argument against my work because not even a single mathematician has found a hole in it.
Write one argument against my work, D, and I’ll show step by step that it is nonsense.
Who is this guy attempting to mimic my name and argument? Must be an ultimate crank like Shadonis.
What a moron, this guy is.
If he was able to publish his ”results” in ”reputable” mathematics journals then I think there are some ”problems/issues” in mathematical publication. Surely, EEE will reply to this 🙂 Can you please send me pdf files of your papers? R YVG BLF DROO HVZIXS NB MZNV RM TLLTOV
Hi Gilbert,
The abstracts and summaries of my papers are in this link: http://users.tpg.com.au/pidro/. You can find the leads there. Try also:
http://esplanaresearch.blogspot.com/2011/11/edgardo-e-escultura-filipino-world.html
can you enumerate and explain the field axioms ?
Look at the original post – the field axioms are listed right there.
I migrated to Australia about five years ago and I’ve been working very hard ever since to go back to Uni and finish a BSc in Maths. The fact that Escultura’s latest link is hosted at TPG (an Australian ISP) fills me with despair. Will I have to migrate elsewhere? I certainly hope not!
Mark CC’s listing of the field axioms is incomplete. Missing in the list is the trichotomy axiom which is false. A complete listing is in Royden’s Real Analysis, pp. 31 – 32.
You have a long way to go, Andres, but if you leave anything beyond your gray matter you won’t get anywhere.
Mark’s listing of the field axioms is complete. It seems that Escultura is talking about another set of axioms by the wrong name (it doesn’t make sense for trichotomy to be a field axiom, because there are unordered fields). I don’t have a copy of Royden handy, but I would guess that it’s the real number axioms: the field axioms as above, plus the ordering axioms: trichotomy, a, b > 0 implies a+b > 0 and ab > 0, and a > b implies a+c > b+c.
We know that these axioms are consistent, because we have a model for them (actually, we have several models).
But. There’s a very big exception. Escultura has mentioned Brouwer a few times, and that’s the clue. In intuitionist logic, the trichotomy axiom fails.
I haven’t read Brouwer closely enough to speak for him with any confidence. My impression is that the intuitionist reals are the same as Turing’s computable numbers. You haven’t got a number unless you have an algorithm for producing it. It doesn’t really matter what the representation is because you can produce an algorithm to convert from one to another, so we might as well consider them to be infinite decimals.
If a is less than b, all we have to do is compare digits from a and b until there’s a difference. But if a is ‘equal’ to b, we’d be comparing digits forever, and never get an answer. My understanding is that this is not allowed.
It seems to me that Escultura has started with intuitionism and then headed off into the wilderness. If you want to engage with him, that’s probably the place to start. But I don’t think he wants to engage.
A complete listing of the field axioms is in Royden’s Real Analysis, pp. 31 – 32. The three axioms of the new real number system is in this link:
http://www.scirp.org/Journal/PaperInformation.aspx?PaperID=63915
The listing of the field axioms agreed by MarkCC and John Fringe is the one found in any high school text book in algebra. It is not complete.
I have read your supposed counter example, it is fallacious from beginning to end and shows you clearly do not understand formal mathematics.
Hang on, this part very nearly makes sense.
It’s true that the real numbers are not completely ordered. This is a well-known fact, illustrated (as EEE has probably pointed out at some point) by the fact that the set {0,1,2,3,…} has no upper bound.
But nobody I know has ever claimed the reals are a complete order, because it’s so obviously wrong. Perhaps EEE is getting “complete order” and “total order” mixed up? (The names are quite confusing, and < on the real numbers is a total order…)
Well, actually…
I hate to say anything that could be interpreted as a defense of EEE. But, in fact, the real numbers are in fact completely ordered in the usual construction of math.
We build math from ZFC set theory. The “C” in ZFC is the axiom of choice, which is a weird bugger. The axiom of choice proves (and in fact is equivalent to) the well-ordering theorem. Well-ordering, in turn, says that in any set, there’s a minimum element.
Look at the set of numbers greater than 0. By the well-ordering theorem, there is a unique number that is the minimum element of that set. Remove that element, and there’s a unique number that is the minimum element of the remaining set. And so on.
I hate the axiom of choice. It just doesn’t make sense to me.
I meant that post as a reply to http://scientopia.org/blogs/goodmath/2011/02/10/e-e-escultura-and-the-field-axioms/#comment-30309, but I screwed up the posting somehow.
EEE was saying that the real numbers under < are "supposedly" a complete, well-ordered field. I know a well-ordering exists (isomorphic to some uncountable ordinal), but the everyday ordering relation < isn't it. My point was that I can't find who is doing the "supposing" in this context. Could be EEE himself…
I found the source fo his non-sense
http://www.dynamicpublishers.com/Neural/NPSC2009/05-NPSC-2009-The%20New%20Real%20Number%20System%20-Modified.pdf
page 61 (by label)